Question: Explain motion of a car on a banked road curve. OR
Explain why in road curves one bank (outer) is higher than the other (inner). OR
Explain banking of roads.
ANSWER
When a car moves round a curve on the road, it tends to slip away from the center of the curvature. However, the friction between the tires and road surface provides the centripetal force which keeps the car on the curve. But the friction has a limit. When the curve is sharp or the road is slippery (e-g, when it is raining), the frictional force is not sufficient to keep the vehicle on the road bend.
Road banking
Road banking is the mechanism by which the centripetal force is increased to an optimal limit so that the car keeps on the road track.
Explanation: When a car moves on a track, the two relevant forces acting on it are;
(i) Weight of the car = mg: This force is always directed vertically upward, irrespective of the surface of the road.
(ii) Normal reaction of the road: This force is always normal to the road. If the road surface is inclined, its direction also changes the same way.
Now consider the figure. Normal reaction of the road surface is making an angle θ with the vertically downward force mg. This angle is equal to the angle of inclination of the road. Resolve the normal reaction force F into rectangular components. It is clear that the component Fsinθ of the normal reaction is providing the necessary centripetal force.
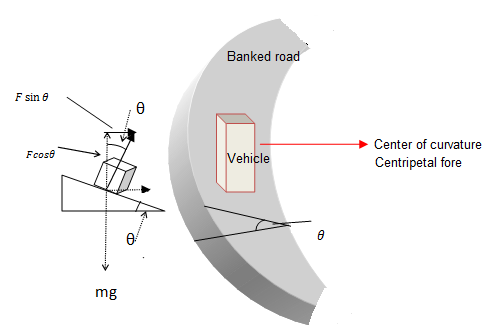
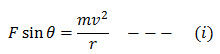
Similarly, the component Fcosθ balances the weight of the car.
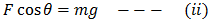
Divide (i) by (ii)
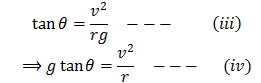
The RHS of the equation is the centripetal acceleration of the car while moving round the road curve of radius r.
Also from equation (iii)
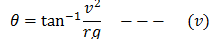
So the banking angle depends upon the speed of the vehicle and not on its weight. Therefore, ideally, the curve can be banked for one particular speed. For greater speeds, force of friction should also be taken into account. If F` is the force of friction acting towards the center of the curve, then,
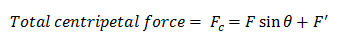

Pingback:angular-motion-different-parameters-of-angular-motion – msa