Question 10: What is meant by Carnot Cycle and Carnot Engine?

ANSWER

Carnot Cycle

A number of processes after the completion of which the properties of the system returns to the original state is called a cycle.
The operating cycle of a Carnot cycle consists of the following four processes.

1.       Isothermal Expansion

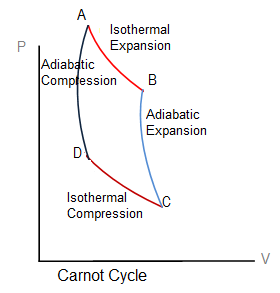
Consider a Carnot heat engine, which consists of a gas cylinder with perfectly insulating walls and perfectly conducting base, having an insulated, weightless and frictionless piston.
Let the initial pressure, volume and temperature of the system are P₁,V₁ and T₁, respectively. Place the cylinder on a high temperature reservoir (HTR). The gas absorbs some amount of heat (+ Q1). With the heat thus provided, the gas expands and the volume increases and pressure decreases. Thus, the temperature remains constant. After the absorption of heat (+Q₁) and the resultant expansion, the state of the gas is described with pressure P₂, volume V₂ and temperature T₁(which is constant). Therefore, the process is isothermal represented by the isotherm A-B in the figure.

2.      Adiabatic Expansion

The cylinder is then placed on a heat insulation stand so that the heat can neither enter nor leave the system. The gas is allowed to expand under these conditions and let the new volume is V₃. With this expansion, the temperature of the gas in the cylinder falls down. Say, it is T₂ now. Similarly, the pressure decreases from P₂ to P₃. The process is an adiabatic expansion and represented by the adiabat B-C in the figure.

3.      Isothermal Compression

The gas cylinder is now placed on cold reservoir (LTR) at temperature T₂. The gas is compressed by increasing the load on the piston. Heat (-Q₂) is rejected by the gas to the LTR and in this way the temperature remains constant. However, the volume decreases from V₃ to V₄ and pressure goes from P₃ to P₄. The process is an isotherm shown by C-D in the figure.

4.      Adiabatic Compression

The gas cylinder is placed on the insulating stand and compressed to the initial stage of P₁, V₁ and T₁. The process is represented by the adiabat D-A in the figure.

The four processes thus complete a Carnot cycle.
In one complete cycle, a Carnot heat engine performs a net amount of work ΔW, and absorbs a net amount of heat Q₁ – Q₂ in the process, represented by the area ABCDA.

Efficiency

Efficiency is defined as,

Since Q and T are proportional, therefore,

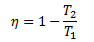
This equation says that the efficiency of a heat engine can never reach to 100%, because T₂/T₁must have some positive numerical value and when subtracted from 1 will make the efficiency η < 1.