Question 4: A sinusoidal alternating voltage of angular frequency ω is connected across a capacitor C. Find the mathematical expressions for the instantaneous voltage, instantaneous current and the average power dissipated per cycle of the applied voltage.

ANSWER

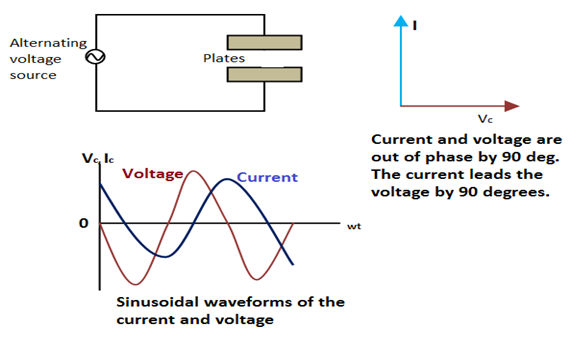
Consider the following diagram. A capacitor of capacitance C is connected to the source of an alternating voltage. When the voltage source is turned ON, flow of the charge begins and one plate begins charging positively and the other as negatively. When the alternating voltage reverses its direction, the charge also does the same. Therefore, an alternating current is always present in the circuit. By definition,

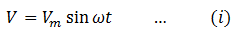
Where V is the instantaneous voltage and V_m is the maximum or peak voltage.

Now we know that Q = CV. Put the value of V from equation (i),

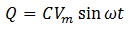
This equation represents the deposit of charge on any of the plates of the capacitor at any moment of time t. Now current is defined as,

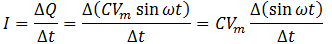
From mathematical calculus, we know that

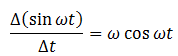
Put this value in the above equation

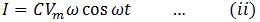
This equation represents the instantaneous value of current in the circuit. As maximum value of cosωt = 1, therefore, maximum current is

If we put this value in equation (ii)

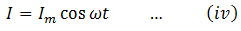
Equation (iv) gives the instantaneous value of the current in the circuit.

Now equation (i) gives time varying voltage and equation (iv) gives time varying current of the circuit. The voltage varies as sinωt and current as cosωt = sin(ωt + π/2). Therefore, there is a phase difference of π/2. The current leads the voltage by 900 = π/2 rad. (This is shown in the phasor and graph in the above diagram).

Power Dissipation

The instantaneous power stored in the capacitor is P = IV = I_mcosωt . V_msinωt. The average power is, therefore, = < I_mcosωt . V_msinωt >. Now for a complete cycle, average of cosωtsinωt = 0, therefore, power dissipated in a complete cycle is zero for a capacitive circuit.

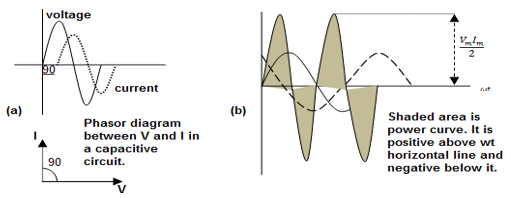
This can be imagined as when the voltage source is charging the capacitor; energy is supplied from the source and stored between the plates of the capacitor. When the voltage reverses its direction, the field strength between the plate’s decreases and energy is returned to the source. Therefore, with the alternating voltage, the energy also fluctuates between the capacitor and the source. For a complete cycle, therefore, the power absorbed is zero.