Question 5: A sinusoidal alternating voltage of angular frequency ω is connected across an inductor of inductance L and resistance R. Find mathematical expressions for instantaneous current, instantaneous voltage, average power dissipated per cycle and draw power curve.

ANSWER

Consider an R-L series circuit as shown. Resistance R and inductance L are connected in series with a sinusoidal alternating voltage source as given in the problem.

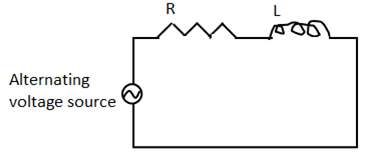
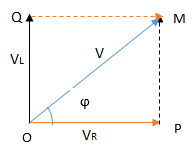
The voltage drop across the resistance V_R (=IR) will be in phase with the instantaneous voltage of the source. Similarly, the voltage drop across the inductor (V_L = IX_L) will be leading the current by an angle of 90⁰. Remember the current is in phase with the V_R. This is shown in the diagram below. </p.

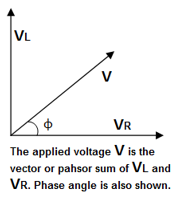
The applied voltage V will be the phasor sum of V_R and V_L. This means the current will still lag the voltage by an angle φ < 90⁰. Therefore,

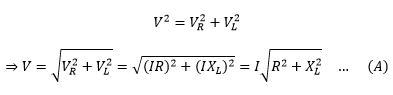
This equation gives the applied instantaneous voltage of the circuit.

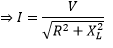
Comparing this with Ohm’s law I = V/R,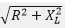

is the total resistance (called impedance) offered by the circuit to the flow of current. Let this be equal to Z, then I = v/z.

This current is in phase with V_R. Looking to the phasor diagram, it can be seen that the current I lags behind the applied voltage V by the angle φ.

The phase angle φ can be determined by the triangle as follow.

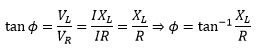
As current is lagging behind the voltage by the angle φ, the current equation for the circuit can be written as

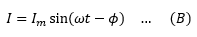
This equation gives the instantaneous current in the circuit.

Power dissipated per cycle

See the phasor diagram. The component of V along the current I is Vcosφ. The power dissipated is
P=IVcosφ … (A)
Here V and I are the r.m.s values of applied voltage and current. The term cosφ is called power factor.

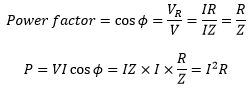
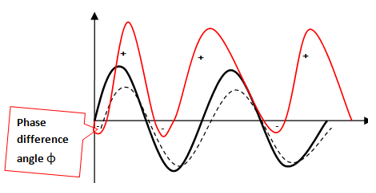
Equation (A) shows some power is consumed by the RL series circuit. This is shown by the negative work in the power graph. However, the area of the positive curve is greater than the area of the negative. Therefore, net power over a cycle is positive.