Question 8: In RL Series Circuit, will the current lag or lead the applied alternating voltage? Explain the answer with a phasor diagram.

ANSWER

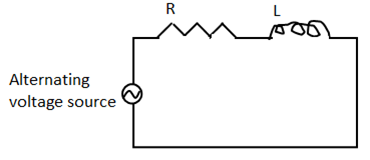
RL series circuit

Electrical circuit containing resistance and inductance connected in series with power source is called an RL series circuit.

Consider a circuit containing resistor R and inductor L connected in series with an AC source.

 We see that

(1) Potential drop across R is in phase with the current at any instant of time.
I = I_msinωt and V = V_msinωt. This is shown in the phasor diagram with V_R and I along the same line (x-axis). The angle between them is 0⁰.

(2) Potential drop across L leads the current by 90⁰. It is shown in the figure on the right. Voltage and current are out of phase by 90⁰.

(3) The applied voltage, V is vector sum of V_R and V_L. It is shown in the figure below.

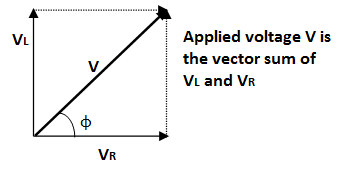
Now it is clear that the current is still lagging behind voltage, but with a different angle, say φ. This is called the phase angle. Obviously, it must lie between 0⁰ and 90⁰ such that 0⁰<φ<90⁰.

Thus if V_L has got a high value, the applied voltage will be closer to V_L which means φ has a greater value close to 90⁰. If V_R has a greater value, φ has a smaller value close to 0⁰.

Calculation of φ

Since applied voltage is the sum of V_L and V_R, therefore,

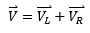
Since they are at right angle to one another, therefore, in terms of magnitudes

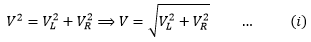
This equation gives the magnitude of the applied voltage.

In order to find the direction of voltage, or the phase angle, which the applied voltage makes with the current, we have

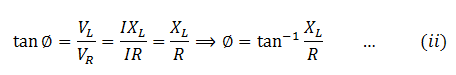
This equation gives the phase angle between the voltage and current of the circuit. Both X_L and R are known, therefore, φ can be calculated through trigonometric methods. If V = V_msinωt , at any instant of time, the instantaneous current is defined as I = I_msin(ωt – φ) .

Thus in an RL series circuit, the current lags the voltage.