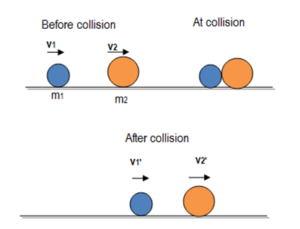
Let two balls of masses m
1 and
If before and after the collision, the motion of the colliding bodies appears on a single line, the collision is said to be one-dimensional or head-on.
m
2, respectively, collide head-on as shown in the figure. Let’s further assume m
1 is approaching towards m
2. Let v
1 and v
2 are their velocities before collision and the final velocities after collision are v
1‘and v
2‘ respectively.
The law of conservation of momentum says that
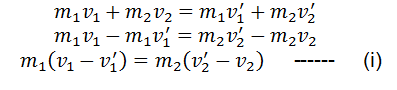
Pingback:Comprehensive Questions, Forces and Motion, Physics Grade 11 – msa