Question 3: Can the electron in the ground state of Hydrogen absorb a photon of energy (a) less than 13.6 ev (b) greater than 13.6 ev? Explain.

ANSWER

When a photon is incident on an electron, the electron absorbs energy of the photon and jumps up to a higher energy state depending upon the amount of energy absorbed. After a short interval of time (10^-8 s) it emits the energy absorbed as electromagnetic radiation and jumps back to a lower energy state.

Similarly, Bohr’s theory, making use of Quantum Mechanics, says the energy states are quantized. So for the electron to raise to a particular energy state, a particular amount of energy would be absorbed.

When energy absorbed is less than 13.6 eV

When the energy of photon is less than 13.6 eV but exactly equal to the difference with the excitation energy of some quantized energy state, then the energy would be absorbed by the electron and would move up to that particular state.

Example

Since the energy of an electron in the nth state is given by

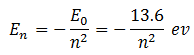
Therefore, energy of electron in the state n = 1 is

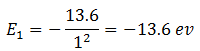
Energy of electron in the state n = 2 is

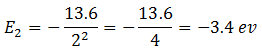
Difference of energies between the two states = -3.4 –(-13.6) = -3.4 + 13.6 = 10.2 eV.

Now let a photon of energy 10.2 eV (which is less than 13.6 eV) is incident on the electron of Hydrogen in the ground state. The electron will absorb the energy of photon and will jump to the next energy state, n = 2.

Therefore, electron in the ground state of Hydrogen can absorb a photon of energy less than 13.6 eV.

When energy absorbed is greater than 13.6 eV

The electron in the ground state of Hydrogen atom will still absorb the photon.

Since the ground state energy of Hydrogen atom is 13.6 eV, therefore, when a photon of energy greater than 13.6 eV is incident on the electron, it will absorb the energy and will ionize the atom. Amount of 13.6 eV will be used to set the electron free of the atom nucleus and the remaining energy would be used as K.E of the electron. The K.E of the electron will move it to an infinite distance from the nucleus of the atom. (Infinite distance is one when it is no more attracted by the nucleus).