Question 3: State the equation of continuity. Show that how it is based on the of conservation of mass? Give two examples from the daily life which are related with the principle of equation of continuity.

ANSWER

Equation of continuity

This principle states that for a steady state flow (i-e, stable flow) the mass flow rate into the volume must be equal to the mass flow rate out.

Mass entering per unit time = Mass leaving per unit time

Equation of continuity is the mathematical expression for the principle of conservation of mass.

Consider an ideal fluid (ideal fluid is one that is incompressible, non-viscous and streamline) flowing through a pipe. The pipe is non-uniform. Consider two cross-sectional areas A₁ and A₂ as shown in the figure.

Let the distance covered by the fluid in a small interval of time Δt after it flows through A_{1 is}

S₁ = v₁Δt

Here v₁ is the velocity of the fluid at A₁.

The volume of fluid ΔV₁ flown through A₁ in time Δt is equal to the cross-sectional area A₁ multiplied by the distance traveled S₁. So,

(By substituting the value of S₁ from the above equation.)

In the same way the distance traveled by the fluid through the other cross-sectional area A₂ in the same interval of time Δt

S₂=v₂Δt

v₂ is the velocity of the fluid at A₂.

But the volume flow through A₂ is (as in the case of A₁),

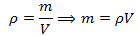
Now we know that density is mass per unit volume, Therefore, the mass of the incompressible fluid flown out through A₁ in time Δt is

Here we have put the value of ΔV₁ from equation (1).

Following the same argument as above, the mass flow through the cross-section A₂ is,

Now the flow of the fluid is steady, the total mass in the tube will be constant. This means the outflow and the inflow are equal. Therefore, Δm₁ and Δm₂ will be equal. Hence equating,

Put the values from the above equations,

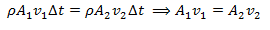
This equation means that cross-sectional area of the pipe multiplied by the velocity of the fluid is always constant.

This equation also can be written as,

This is an important result of the equation of continuity which states,

The speed of any fluid is inversely proportional to the cross-sectional area of the pipe. If the pipe is narrow the speed of fluid will be greater and if the pipe is wider the speed will be slower.

Do you know what is compressible and what is incompressible?

Take a balloon filled with air. Then take some water in a tub. Press both of them. What happens?

Water is incomprssible and gas (air) is compressible!

Compressible and incomprehensible