Question 5: Derive First equation of motion.

ANSWER

First equation of motion is derived with the help of the definition of acceleration.

Suppose, a body of mass ‘m’ moving with an initial velocity v_i and it undergoes an acceleration for time‘t’ seconds so that its final velocity is v_f.

Now according to the definition of acceleration,

Acceleration = change in velocity/time

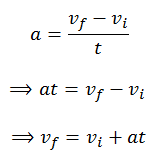
This is first equation of motion.