MCQs on Vectors and Scalars
(1) The direction of a vector in space is specified by
(a) One angle (b) 2 angles (c) 3 angles (d) none of these
(2) A vector can be multiplied by a number. The number may be
(a) Dimensionless (b) dimensional scalar (c) negative (d) all of them
Hint:
- Any real number is a dimensionless quantity. Vector can be multiplied by any real number.
- Mass is a dimensional scalar. We know that mass can be multiplied with velocity (a vector) to give momentum (= mv).
- When multiplied by a negative number, the direction of the vector is also reversed.
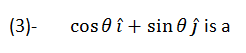
(a) Scalar quantity (b) position vector (c) null vector (d) unit vector, direction θ with x-axis
Hint: Find the magnitude by applying
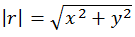
(4)- Maximum number of the components of a vector is
(a) One (b) two (c) three (d) infinite
Hint: A vector may be the sum of an infinite number of vectors. All of them are called components of the vector. However, the rectangular components is a special case in which there are two (or three?) vectors perpendicular to one another.
Do you know any real number can also be the sum of an infinite number of real numbers, 10 = 1+2+3+0.5+.000001+.3+………. Etc.
(5)- Maximum number of the rectangular components of a vector in space is
(a) 1 (b) 2 (c) 3 (d) infinite
Hint: We are talking about a vector in space. If we are concerned with a vector in a plane, then the maximum number of rectangular components would be 2.
(6)- The resultant of two forces of equal magnitudes is also equal to the magnitude of the forces. The angle between the vectors is
(a) 300 (b) 600 (c) 900 (d) 1200
Hint: See question 2 in comprehensive questions.
(7)- In which quadrant the two rectangular components of a vector have same sign
(a) 1st (b) 2nd (c) both 1st and 3rd (d) 4th
(8)- Two vectors A and B are making angle θ with one another. The scalar projection of B on A is written as
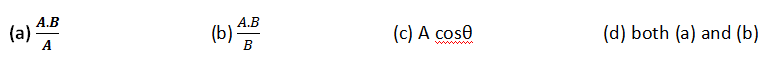

(9)- If A = B, which one is correct
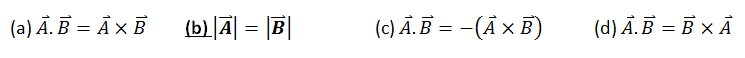
(10) Position vector is defined as the vector which determines the position of a point in space or in a plane with respect to
(a) Another vector (b) space (c) origin (d) its magnitude
(11)- Null vector is a vector with zero magnitude and
(a) Parallel direction (b) perpendicular direction (c) virtual direction (d) arbitrary direction
(arbitrary may be considered as undefined)
(12)- A resultant vector is a single vector which has the same effect as the
(a) Combined effects of the vectors to be added
(b) Perpendicular effects of the vectors to be added
(c) Individual effects of the vectors to be added
(d) None of these
(13) Rectangular components of a vector are always mutually
(a) parallel (b) anti parallel (c) perpendicular (d) arbitrary
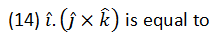

(Try to do other such products of unit vectors).
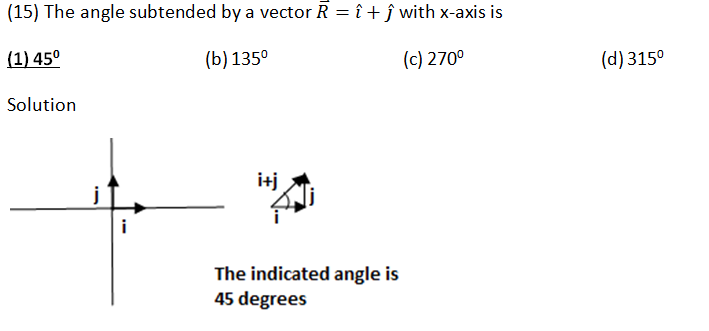
(Try to do more such additions of unit vectors). Remember both i and j in this case have unit magnitude.
(16) Two forces having magnitudes of 10 N and 8 N are added. Which one cannot be the result of their possible sum?
(a) 9 N (b) 18 N (c) 21 N (d) 2 N
Hint: When two vectors are added together, the maximum resultant so obtained is possible only when the two vectors are acting in the same direction, that is, when the angle between them is zero. In such a case the magnitude of the resultant is the sum of the magnitudes of the vectors to be added. So the maximum magnitude of the resultant of two forces of 10 N an 8 N would be 18. Any value greater than 18 N is not possible.
(17) Two forces having magnitudes of 10 N and 8 N are subtracted. Which one cannot be the result of their possible sum?
(a) 9 N (b) 18 N (c) 1 N (d) 2 N
Hint: When two vectors are subtracted, the minimum resultant so obtained is only when the two vectors are acting anti-parallel (in opposite directions). In such a case the minimum magnitude of the resultant is obtained by subtracting the magnitude of one from the other. So the minimum resultant obtained by the subtraction of 10 N and 8 N is 2 N. So 1 N, option 3, is impossible to be obtained.
(18) Tow concurrent forces have a maximum resultant of 100 N and minimum of 80 N. Magnitudes of these forces are
(a) 100 N, 20 N (b) 100 N, 80 N (c) 100 N, 120 N (d) 90 N, 10 N
Hint: Forces are said to be concurrent if their lines of action intersect at one point.
Hint 2: Maximum resultant is obtained when the forces are acting in the same direction. In such case, maximum resultant = magnitude of one + magnitude of the second
(19) The minimum number of forces that can keep a body in equilibrium is
(a) One (b) two (c) three (d) four
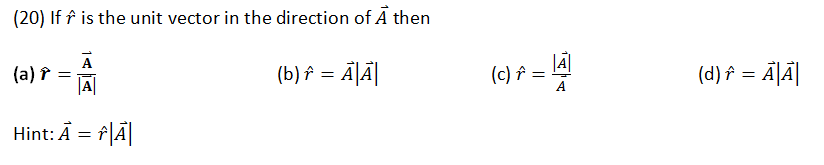

When the vectors are parallel, θ = 0 and sinθ = 0. So is the product.
When A = 0 Or B = 0, the product is zero in both cases.
(22) The greater the force larger will be the
(a) the center of gravity (b) axis of rotation (c) torque (d) moment arm
Hint: Torque is directly proportional to the force applied. See formula.
(23) Clock-wise rotation is taken as
(a) Positive (b) negative (c) neutral (d) important
(24) Two forces which are equal in magnitude, opposite in direction and not acting along the same line is a
(a) Rotation (b) parallel (c) single (d) couple
(25) When the net torque acting on a body is zero, which of the following will be constant
(a) angular momentum (b) linear momentum (c) moment arm (d) force
(26) The daily rotation of earth about its own axis, rotation of flywheel about its axis and a rotating top are good examples of
(a) Circular motion (b) rotatory motion (c) orbital motion (d) spin motion
(27) Larger the moment arm, larger will be
(a) Momentum (b) Torque (c) Linear momentum (d) none
(Recall the equation for the torque).
(28) A body is said to be in dynamic equilibrium
(a) When it is in uniform motion along a straight line (b) when the acceleration changes
(c) When it is in uniform motion along a circle (d) none
(29) The second condition of equilibrium says “a body is said to be in equilibrium when the vector sum of all torques acting on it is
(a) zero (b) maximum (c) minimum (d) moderate
(30) The two forces which form a couple
(a) are perpendicular to each other (b) can be replaced by a single equivalent force
(c) cannot be replaced by a single equivalent force (d) are parallel
Note: Remember a single force cannot produce a couple.
(31) Direction of torque is
(a) the same as the direction of the corresponding applied force (b) opposite to the direction of applied force (c) Perpendicular to the direction of the applied force (d) none
Explanation: As cross product of F and r, torque is perpendicular to both F and r.
(32) Every point on a rotating body has
(a) Same linear momentum (b) same linear velocity (c) none of these (d) Angular velocity
(33) In the system international the unit of angular momentum is
(a) kg s (b) j s (c) N s (d) N m
(34) The torque has magnitude equal to the magnitude of the product of force and moment arm and has direction
(a) 1800 to the plane of force and moment arm (b) 3600 to the plane of force and moment arm
(c) 00 to the plane of force and moment arm (d) 900 to the plane of force and moment arm
(35) A body in equilibrium is
(a) always at rest (b) can move with constant acceleration (c) can move with constant velocity (d) can move with constant and variable acceleration
(36) Jumping of a paratrooper from an helicopter is an example of
(a) Static equilibrium (b) dynamic equilibrium (c) all equilibriums (d) none
(37) If the vector sum of torques acting on it is zero, the body is said to be in
(a)Rotational equilibrium (b) equilibrium (c) static equilibrium (d) translatory equilibrium
(38) In static and dynamic equilibrium, the body does not possess any
(a) Acceleration neither linear nor angular (b) velocity neither linear nor angular
(c) Displacement neither linear nor angular (d) none
(39) Torque is defined as the time rate of change of
(a) Linear velocity (b) Angular momentum (c) Linear momentum (d) Angular velocity
