Question 4: In light of first law of thermodynamics, describe,

Isochoric Process

·         Isobaric Process

Isothermal Process

·         Adiabatic Process

Answer

Isochoric Process

A thermodynamic process in which the volume of the system remains constant is called an isochoric process.

Consider a gas contained in a cylinder. The base of the cylinder is conducting so that heat can be transferred through it. The walls of the container and the piston are non-conducting for heat. Furthermore, the piston is fixed and cannot move. In this way, the volume of the gas remains constant.

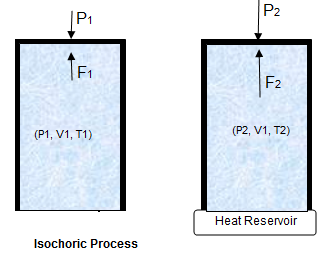
Now let us suppose P₁,V₁ and T₁ are the initial pressure, volume and temperature of the gas, respectively. Let we pass on some amount of heat ΔQ to the system. The system can neither expand nor contract, therefore, no work is done by or on the cylinder and ΔW = 0. Apply First Law of Thermodynamics,

ΔQ = ΔU + ΔW
⇒ ΔQ = ΔU

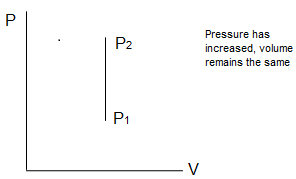
This means that the heat provided to the system is entirely used in increasing the internal energy of the system. The pressure and temperature of the system will increase.
In the same way, removal of heat from the system under isochoric conditions will decrease the internal energy. The system will cool down and pressure decreased.

Isobaric Process

Thermodynamic process during which the pressure remains constant is called isobaric process. Consider a gas contained in a cylinder. The base of the cylinder is heat conducting whereas the walls are non-conducting. The frictionless piston on the cylinder has a cross-sectional area ‘A’.
Now suppose P₁, V₁ and T₁ are the initial pressure, volume and temperature respectively, of the system. Let the gas is heated, a certain amount of heat ΔQ is transferred to the system. The gas expands and pushes the piston upward to a small distance ΔY so that the pressure does not change to a significant amount.

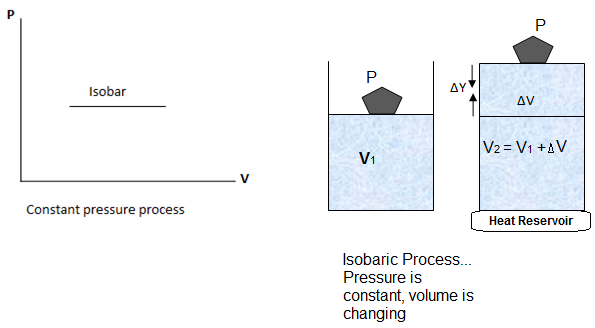
Now if T₂ and V₂are the temperature and volume after expansion. The work done by the gas is

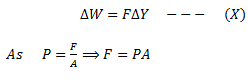
Put this value of F in equation (X)

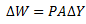
Since, AΔY = ΔV, therefore,

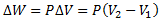
ΔV being the small change in volume after expansion.

Applying first law of thermodynamics

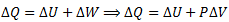
The graph of an isobaric process is a straight line parallel to the volume axis (i-e, constant pressure) and called isobar.

Isothermal Process

Thermodynamic process in which the system undergoes changes but the temperature remains constant is called isothermal process.

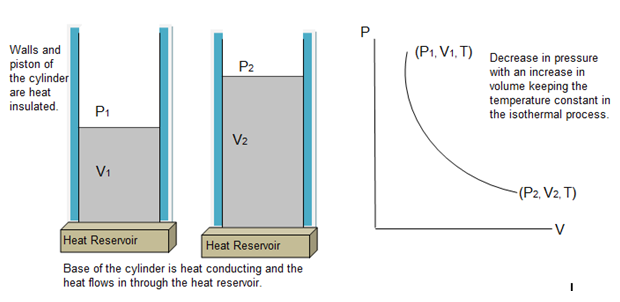
Consider an ideal gas contained in a cylinder of conducting base and non-conducting walls and provided with a movable piston on top. The cylinder is placed on a heat reservoir at temperature T.
Now allow the gas to expand slowly by decreasing the pressure on the piston.This will decrease the temperature of the gas. As heat is provided by the heat reservoir, the temperature of the gas remains constant. The pressure will decrease, the volume will increase and the temperature will remain constant. If we consider any two states at P₁, V₁, T and P₂,V₂, T (T is constant), the graph will be a continuous curve. Such a curve is called isotherm.

 Applying First law of thermodynamics,

ΔQ = ΔU + ΔW

Since temperature is constant, ΔU = 0, therefore,

ΔQ = ΔW

This equation indicates that the gas does work by expanding and an equal amount of heat is supplied by the heat reservoir and the temperature remains constant.

On the other hand, if the gas contracts, work is done on the system and an equal amount of heat leaves the gas.

Adiabatic Process

Thermodynamic process in which no heat enters or leaves the system is called adiabatic process.

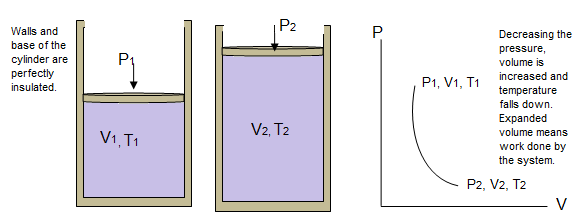
Consider an ideal gas contained in a perfectly insulated cylinder having a movable heat insulated piston on the top. Since no heat can enter or leave the system, so if the gas is expanded quickly, the temperature will fall down.

Now if the pressure is decreased on the piston and the gas is allowed to expand, the temperature will decrease.
Applying First Law of Thermodynamics,

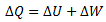
As no heat can enter or leave the system, ΔQ = 0, therefore,

0 = ΔU + ΔW ⇒ ΔW = -ΔU

This means that work is done at the cost of internal energy of the system. The equation may also be written as,

ΔU = -ΔW

In which case work is done on the system increasing its internal energy.

The graph under adiabatic conditions is a curve called adiabate.

Note: A truly adiabatic process is an ideal one. However, proper insulation of the system and performing the process quickly enough may be helping.