Problem 2: Water travels through a 9.6 cm diameter fire hose with a speed of 1.3 m/s. At the end of the hose, the water flows out through a nozzle whose diameter is 2.5 cm. (a) What is the speed of water coming out of the nozzle? (b) What diameter nozzle is required to give water speed of 21 m/s?
Solution
Given Data
Dia of the pipe = 9.6 cm = 0.096 m ⇒ radius of the pipe = 0.096 ÷ 2 = 0.048 m
Since Area = πr2, therefore, area of cross-section of the pipe = 3.14 × (0.048)2 = 3.14 × 0.048 × 0.048 = 0.00723 m2
Dia of nozzle = 2.5 cm = 0.025 m ⇒ radius of the nozzle = 0.025 ÷ 2 = 0.0125 m2
⇒ Area of the cross-section of the nozle = 3.14 × 0.0125 × 0.0125 = 0.00049 m2
Speed of water in the pipe = 1.3 m/s
Required: (a) Speed of water at nozzle end
Formula: Equation of continuity, A1v1 = A2v2
Apply this formula with A1 = Cross-sectional Area of the pipe, v1 = speed of water in the pipe, A2 = Cross-sectional area of the nozzle and v2 = speed of water at the nozzle.
Part (b): We have to find the diameter of the nozzle if the speed of outcoming water is 21 m/s. If ‘r’ is the radius of the nozzle, then area of the cross-section of the nozzle will be A2 = πr2. For convenience, we put area of the pipe as A1 = π r12, where r1 = 0.048 m = radius of the cross-section of the pipe. Therefore,
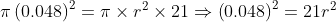
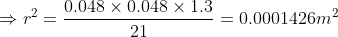
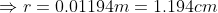
Since diameter is 2 times the radius, therefore,
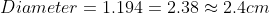
This is the answer.