Question 3: Does a moving charge experiences a force in the magnetic field? Explain.

ANSWER

 We know that a moving charge is associated by a magnetic field around it. When such a moving charge enters a magnetic field, the two fields interact and as a result the moving charge is experiencing a force.

For a positive charge q introduced perpendicularly into a magnetic field B, it is observed that

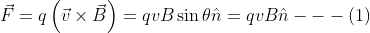
Here v is the velocity of the charge q and θ is the angle between velocity and magnetic field (it is 90 deg in this case).

The unit vector n is in the direction of force experienced by the charge and can be determined by the Fleming’s Left Hand Rule. Under the action of this force, the charge will follow a circular path. Here, we note that the magnetic field neither speeds up nor slows down the particle but deflects the particle side way only. Therefore, the particle moves under the influence of constant magnetic force which provides the necessary centripetal force to the particle to keep it on the circular path.

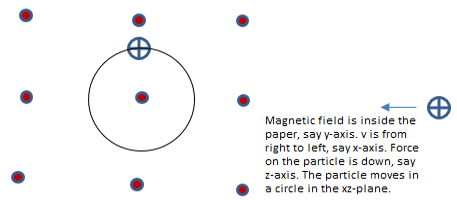
Now if ‘r’ is the radius of the circular path and ‘m’ is the mass of the charged particle, the centripetal force is

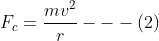
Equations (1) and (2) are same. So comparing the magnitudes,

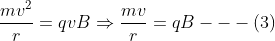
Since v/r = ω (angular velocity). Put this value in the above equation.

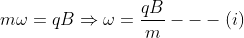
In the same way, radius of the circular path can also be found from the above equation (3).

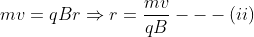
Similarly, time period T of the particle can also be calculated.

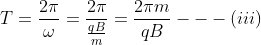
And the frequency ‘f’ is the reciprocal of time period.

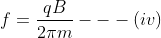
This frequency is called cyclotron frequency.

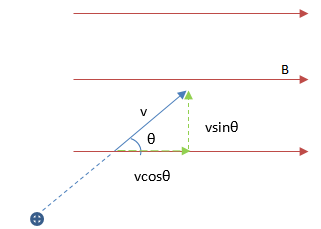
If the charge enters the field at certain angle θ other than 90^o, then the particle moves along a spiral path. In fact the velocity components V sinθ moves the particle vertically and the component V cosθ moves it horizontally and the combined effect is a spiral trajectory. The deflection of charge particle in a magnetic field is used in television tubes, electron microscope, spectrographs and charged particle accelerators.