Question 5: Define molar heat capacities of Cp and CV for a gas. Show that for a mole of an ideal gas Cp – CV = R
ANSWER
Let we have 1 kg of a substance at a certain temperature. We provide heat ΔQ to this substance and the temperature of the substance rise by 1K. This amount of heat ΔQ is called the specific heat of the substance.
Molar Specific Heat
The quantity of heat required to raise the temperature of one mole of a gas by 1K is called molar specific heat or molar specific heat capacity of that gas.
For a gas, we have two specific heats; specific heat at constant pressure, Cp, and specific heat at constant volume, Cv.
Specific Heat at constant volume, Cv
The amount of heat required to raise the temperature of one mole of a gas by 1K while keeping the volume constant is called constant volume molar specific heat (molar specific heat at constant volume) of that gas.
Suppose ‘n’ moles of an ideal gas are confined in a cylinder provided with a fixed piston. When heat is provided to the gas, the volume remains constant and all the heat provided goes to increase the kinetic energy of the gas. Correspondingly, the temperature of the gas also increases.
If the amount of heat provided is ΔQv and increase in temperature is ΔT, then molar specific heat at constant volume is given by,
ΔQv = nCvΔT
CV is the molar specific heat at constant volume.
Specific Heat at constant pressure, Cp
The amount of heat required to raise the temperature of one mole of a gas while keeping its pressure constant is called molar specific heat at constant pressure, Cp, of that gas.
Now consider ‘n’ moles of an ideal gas contained in a cylinder provided with a movable piston. When the gas is heated its temperature rises and at the same time the gas expands and pushing the piston upward, doing work on the surrounding.
If ΔQp is the amount of heat provided to ‘n’ moles of the gas and rise in temperature is ΔT, then,
ΔQp = nCpΔT
Here Cp is the molar specific heat capacity at constant pressure.
To prove that Cp – Cv = R
By definition of constant volume molar specific heat,
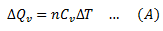
As the volume is constant, there is no work involved in the process.
Applying First Law of thermodynamics for this situation,
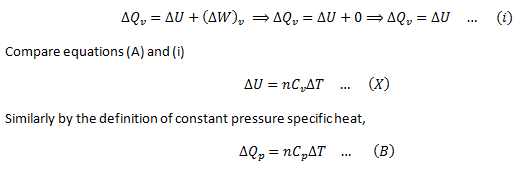
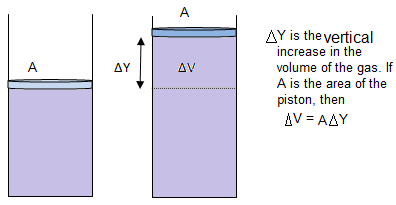
As the gas can expand by applying heat to it, therefore,doing work on the environment. Therefore, if ΔQp is the heat provided and ΔWp is the work done, then, applying first law of thermodynamics,
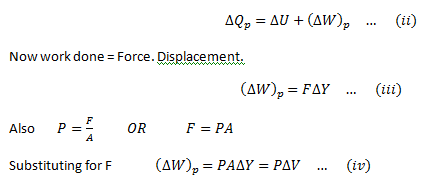
For an ideal gas, the general gas equation is,
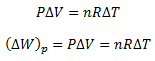
Substitute this equation for the work done in equation (ii)

