Question 8: State and explain Heisenberg’s uncertainty principle. Justify the validity of this principle by a thought experiment.

ANSWER

Heisenberg’s Uncertainty Principle

It is impossible to determine the position and momentum of a particle simultaneously with a perfect accuracy even with an ideal instrument.

Explanation

Applying the quantum mechanics, Heisenberg gave this principle first in 1927. The uncertainty principle is a consequence of the fact that any measurement of a system must disturb the system under investigation with a resulting lack of precision in the measurement. So it is impossible to exactly specify the position and momentum of a particle at a certain instant of time. This limit of accuracy is not due to any technical difficulties in the experiment but due to the dual nature of waves and particles.

Justification of the principle by a thought experiment

Suppose we want to measure the momentum of an electron. We need to make it visible for observation. Therefore, we fall some light on it. Now light consists of photons. When these photons are incident on the electron, they impart some momentum to the electron. So now, when we measure the momentum of the electron, it is not the original momentum, which the electron possessed before illuminating. So the photon (particle) nature of light has disturbed the momentum of the electron which we wanted to measure. (Please note that when light interact with small particles like electrons, it behaves like particles). This makes our measurement an inaccuracy. The inaccuracy must be of the order of the momentum of photon, h/λ.

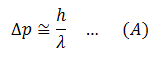
In the same way, when the photon hits the electron, the photon is scattered with less energy and the electron recoils with some extra K.E energy and changed position. The change in the position of the  electron will be of the order of the wavelength of the incident photon of light. Therefore,

Now to reduce the uncertainties, we consider equations (A) and (B).

To reduce the uncertainty in the change in momentum, we should use light of large wavelength (because λ is in the denominator). But using a larger wavelength increases uncertainty in the position (from equation B where λ is in the numerator). Multiply (A) and (B)

This is the mathematical form of the uncertainty principle. It states that the product of uncertainties in the momentum and position of a body is equal to the Plank’s constant, h.