Question 6: Explain the term impedance of an AC circuit. Find expression for the impedance of the RLC series circuit.
ANSWER
Impedance
An AC circuit may consist of a resistor R, a capacitor C and inductor L in combination. The combined opposition offered to the flow of AC current by these elements is called impedance. It is defined as,
“The ratio of the rms value of the applied voltage to the rms value of the resulting current.” Mathematically,

Z being the impedance of the AC circuit.
Unit of impedance
Unit of impedance is ohm, denoted by Ω. . Impedance of a circuit is said to be one ohm if a current of one rms Ampere flows in the circuit when the voltage across its terminals is one rms volts.
Impedance of the RLC series circuit

Consider resistance R, inductance L and capacitance C connected in series in an AC circuit. We note that;
- Potential difference VR across the resistance R is in phase with the current and given by
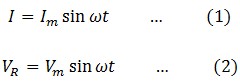
-
Voltage VL across the inductance L leads the current by π/2 rads.
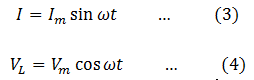
-
Voltage drop across C is lagging behind the current by π/2 rad.
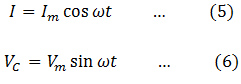
Therefore, VL and VC are out of phase by π rads. This is shown in the vector diagram.

Impedance calculation
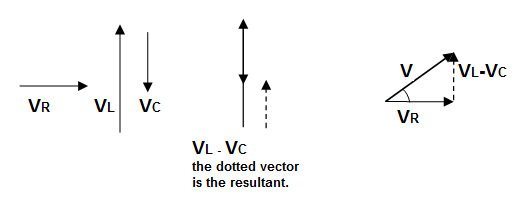
The applied voltage is equal to the vector sum of VR, VL and VC. Let VL>VC, then their sum is VL – VC which is directed in the upward direction along VL. The net applied voltage is, therefore, somewhere in the first quadrant between VL and VR as shown in the figure.
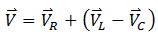
The magnitude of the applied voltage is

Now we know that VR = IR, VL = IXL and VC = IXC. Therefore, the above equation can be written as
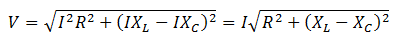
Total impedance of the circuit is
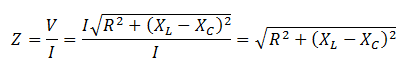

For this particular arrangement (XL>XC), the voltage is leading the current by an angle φ, called the phase angle. However, when XC>XL, the voltage is lagging behind the current. Both the situations are depicted in the diagram to the right. These are called impedance triangles.

Pingback:lq-ch-15-p12 – msa