Question 5: Use properties of continuous function to test the continuity and discontinuity of the following functions:
Solution
a. f(x) = 2x – 3
Suppose x = a ∈ R and apply the conditions of continuity of a function.
A function f(x) is said to be continuous at x = c, if all the following three conditions are met;
(i) The function is defined at x = c, that is, f(x) exists at c.
(ii) The function approaches a definite limit as x approaches c, that is, limx→c f(x) exists.
(iii) The limit of the function is equal to the value of the function when x = c, that is, limx→cf(x) = c.
(i) f(a) = 2a – 3
Since ‘a’ is a real number, therefore, the RHS of the equation is a real number. Therefore, f(x) exists at ‘a’.
(ii)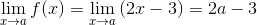 
. Therefore, the limit exists.
(iii)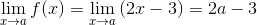
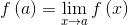
Therefore, f(x) = x – 3 is continuous for all x ∈ R.
Let a ∈ R.
(i) g(a) = 3 – 5a (This is a real number).
(ii) limx→a g(x) = limx→a (3-5x) = 3-5a (limx→a g(x) exists.
(iii) g(a) = limx→a = g(x)
The given function is continuous for all real numbers.
c. 
If we put x = 5, the function is h(5) = 2/(5-5) = 2/0. This is undefined. Therefore, the function doesn’t exist at x = 5. Therefore, it is discontinuous at x = 5.
d. 
If we put x= -3, the function is k(-3) = -3/0. This is undefined and therefore, doesn’t exist at x = -3. Therefore it is discontinuous.
e. 
The function is undefined and discontinuous at two points, x = 3 and x =-2.
f. 
The function is indeterminate at two points, x = 0 and x = -7. Therefore, it is discontinuous.
Pingback:Math’s 12, Exercise 1.4