
Select the correct answers for the following questions.
1. The expression for escape velocity is given by

Solution
The initial velocity which a projectile must have at the surface of earth in order to go out of earth’s gravitational field is called escape velocity. In order to calculate the escape velocity, we know that the work done required to lift a body from earth’s surface to a far off distance where it is not influenced by the force of gravity is
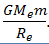
Where m = mass of the object
Me = mass of the earth
G = Gravitational constant.
Hence, if a projectile is given an initial KE equal to this, it will reach to an infinite distance and escape out of the gravitational field. So, if vesc is the escape velocity at earth’s surface, then
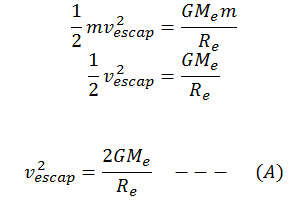
We know that,
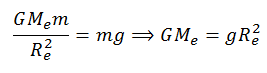
Put this value of GMe in equation (A),
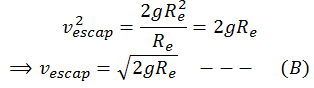
2. An example of non-conservative force is
(a) Electric force (b) Gravitational force (c) Frictional Force (d) Magnetic force
Solution
Conservative force is one which doesn’t depend on the path followed. Consider the most common case of gravitational field. If you want to lift a body of mass m from a point A in the gravitational field to some other point B in the gravitational field, you can take a number of paths. The path may be a zigzag, a curve or a straight line. However, in all cases the work done against the gravitational force (vertically down) is same. This work done is stored in the body as its gain in potential energy, mgh. Another point to remember about conservative forces is that “stored energy” or potential energy can be defined only for conservative forces.
Apart from gravitational force, electrostatic force and magnetic force is also conservative; obeying the above-mentioned rules.
On the other hand there are forces which are dissipative (dissipative means dispersed or diffused) which means they cannot be stored (like in the case of P.E in the above example). Such forces are called non-conservative forces. Friction is a common dissipative or non-conservative force. Another example may be air resistance when a body moves in the surrounding air).
3. The energy stored in the spring of a watch is
(a) K.E (b) Electrical Energy (c) Elastic P.E (c) Solar Energy
Remember an object raised (or changed) in position is not the only reason for gaining P.E. There are some other methods which also impart P.E to objects. One of them is elastic P.E.
Consider the situation when an object is deformed and it returns to its original shape like a rubber chord. When a rubber chord is extended by applying a force (deformed) it restores to its original position when the force is removed. In the deformed shape the body posses energy. This type of energy is called elastic P.E. (You know elasticity is the property of a substance due to which it restores its original dimensions).
4. One horse power is given by
(a) 746 watts (b) 746 joules (c) 746 KW (d) 746 Foot Pound
5. Work is said to be negative if F and d are
(a) Parallel (b) Anti-parallel (c) Perpendicular (d) none of these
Explanation: When force F and displacement d are anti-parallel, the angle between them is 1800 and cos θ = -1. Therefore, work done is negative.
6. Two bodies of masses m1 and m2 have equal momentum; their kinetic energies are in the ratio

Solution
Let p1 is momentum of m1 and p2 is momentum of m2.
Then according to the condition of the problem;
p1 = p2 = p ——- (A)
Let v1 is the velocity and E1 is the kinetic energy of m1.
Then p1 = m1v1 ——- (1)
p12 =m12v12 ——- (A)
And E1 = ½ m1v12 —— (2)
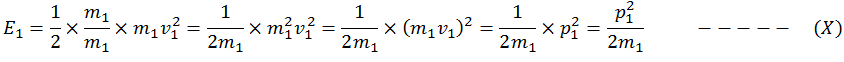
Let v2 is the velocity E2 is the kinetic energy of m2.
Then p2 = m2v2 ——- (3)
p22 = m22v22 ——— (B)
And E2= ½ m2v22 ——- (4)
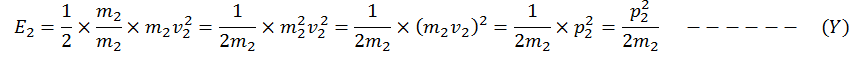
Now divide (X) by (Y)
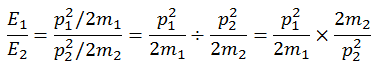
Now p1 = p2 = p (equation A). So substitute in the above equation

Cancel the same factors of 2 and p,
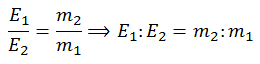
7. The atmosphere is held to the earth by
(a) Winds (b) Gravity (c) Clouds (d) The rotation of earth
Explanation
Atmosphere is the layers of gases (mostly Nitrogen and Oxygen) surrounded by the earth (or any other planet). These gases are held in the space around the earth by the gravitational force of the earth. Atmosphere means the sphere of vapors and is not confined to the case of earth. Any planet or a huge mass may have an ‘atmosphere’.
8. If momentum is increased by 20% then K.E increases by
(a) 44% (b) 55% (c) 66% (d) 77%
Solution
Let initial momentum = pi = 1 .We know the K.E in terms of momentum
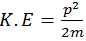
(See MCQ 6 for the proof)
Therefore, initial K.E = (K.E)I = 1/2m
Final momentum with a 20% increase
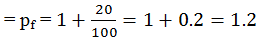
Therefore, final K.E
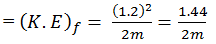
Increase in K.E
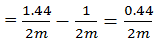
% increase in K.E
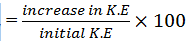
Put the values
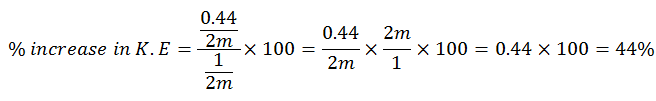
9. If K.E of the body becomes four times the initial value, then the new momentum will
(a) Become twice its initial value
(b) Become three times its initial value
(c) Remains constant
(d) Become four times its initial value
Solution :Relation between K.E and momentum is
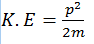
Let initially, p is the momentum and K.E is the kinetic energy, then
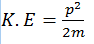
Let momentum is p’ when K.E undergoes a 4 times increase. Then
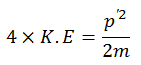
Put the value of K.E,
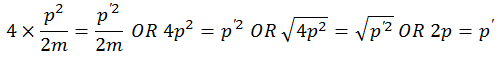
So the new momentum is twice the initial momentum.
10. Two bodies with K.E in the ratio of 4:1 are moving with equal linear momentum. The ratio of their masses is
(a) 1:2 (b) 1:1 (c) 4:1 (d) 1:4
Solution
Given that
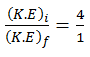
Since
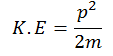
Let m1 is the mass of one body and m2 is the mass of the other. Since their momentum’s are of equal, say p.
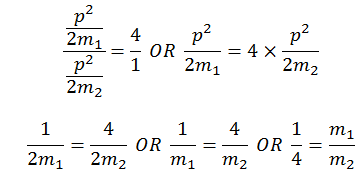
Therefore
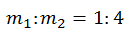
11. A body of mass 5 kg is moving with a momentum of 10 kg ms-1. A force of 0.2 N acts on it in the direction of motion of the body for 10 seconds. The increase in its kinetic energy is:
(a) 2.8 joules (b) 3.2 joules (c) 3.8 joules (d) 4.4 joules
Solution
m = 5 kg p = 10 kg ms-1
K.E = p2/2m = 100/10 = 10 J
Since p = mv, therefore, 10 = 5v OR v = 2 ms-1
This is the initial velocity.
Now force = F = 0.2 N, Time = t = 10 sec
F = ma OR a = F/m = 0.2/5 = 0.04 ms-2
Final velocity = vf = 2 + 0.04 * 10 = 2 + 0.4 = 2.4 ms-1
Final momentum = 5 * 2.4 = 12 kg m/s
Final K.E = 12*12/10 = 144/10 = 14.4 J
Change in K.E = 14.4 – 10 = 4.4 J
12. If force and displacement of a particle in the direction of force are doubled. Work would be:
(a) Doubled (b) 4 times (c) half (d) ¼ times
Solution
Try yourself.
Hint: W = Fd
Double the force and displacement as 2F and 2d. Find Wf = 4Fd = 4Wi

Pingback:numerical-problems-on-work-power-and-energy-physics-11 – msa
Pingback:index-sq-ch4-p11 – msa
Pingback:Work, Power and Energy, Comprehensive Questions – msa