Question 2: Define mean, peak and rms value of sinusoidal voltage and sinusoidal alternating current. Obtain mathematical expression for the rms value of current.

ANSWER

Peak Value

The highest value of sinusoidal voltage or sinusoidal current in one cycle is known as peak value.

We know that the sinusoidal quantity like alternating voltage or current, increases with time so that it attains maximum value after some time. Then it gradually decreases, passing zero, reaches a maximum negative value. Therefore, peak values occur twice in one cycle.

Mean value

The mean, or average, value of a sinusoidal waveform is the average of all its values over one cycle.

In case of a periodic waveform (which repeats after some times), the average or mean value of a symmetrical alternating current or voltage (symmetrical means that the quantity spreads to equal extents above and below the horizontal axis), is zero.

Root Mean Square (rms) value

The square root of the mean squared values is known as rms value of sinusoidal current or sinusoidal voltage. ALTERNATIVELY, it is the square root of the mean of the instantaneous values of a sinusoidal quantity (voltage or current).

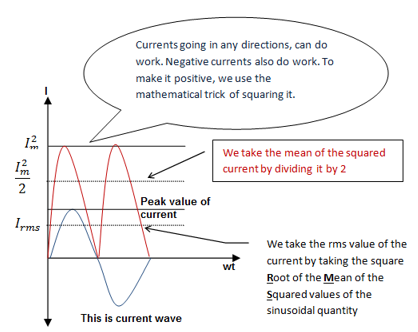
Mathematical expression for the rms value of current

The equation for a sinusoidal alternating current is

Power delivered to a resistance by this current is

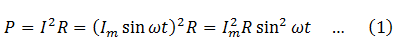
Now the sine value varies between 0 and 1. Therefore, its average is (0+1)/2 = ½. Put this value in equation (1) to get average power of the current.

Now if I_rms is the effective value of the alternating current, then

Compare (2) and (3)

Therefore, the RMS or effective value of the current is 00.707 times the peak value of the alternating current.