Problem 1.2:  The length and width of a rectangular plate are (15.6 ± 0.1) cm  and (10.80 ± 0.01) cm  respectively. Calculate the area of the plate and uncertainty in it.

Solution

Given: Length of the plate = (15.6 ± 0.1)cm
Width of the plate = (10.80 ± 0.01)cm

Required: Area of the plate = A, and uncertainty in the area = ΔA

Strategy: In order to calculate uncertainty in the measurement of the area of the plate, we apply the product rule of calculating uncertainty in the final result.

Hint: See question 4 in comprehensive questions, part (2) rule for uncertainty in product.

Area of the plate = length × width, therefore,

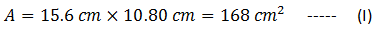
(Note: Remember, in multiplication and division, the final result has sig figs equal to the number with least significant numbers. Here it is 15.6 with sig figs 3).

To find uncertainty in the calculation of the area of the plate, we use the rule;

% uncertainty in the area = ± (%uncertainty in length + %uncertainty in width)

% uncertainty in length:

Length of the plate = 15.6 cm

Uncertainty in length = ± 0.1

% uncertainty in length=

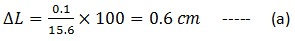
(Note: Rounded off up to 1 figure, as per rules).

% Uncertainty in width:

Width of the plate = 10.80 cm

Uncertainty in width = ± 0.01 cm

% uncertainty in width =

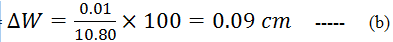
Put the values from (a) and (b) and use the above rule, % uncertainty in the area = ±(0.6+0.09) =0. 69

This is the uncertainty in 100 cm² of the plate area (% uncertainty). We are concerned with 168 cm² of the area of the plate (equation I). Therefore to calculate uncertainty in 168 cm², we have,

Uncertainty in the area of the plate =

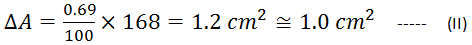
Equations (I) and (II) give the required results.

Do you know how the exact area of the plate can be calculated? It would be A = (168.48 ± 1.23) cm²