Problem 1.4: Theory suggests that drag force depends upon the viscosity of the medium, average radius of the object and velocity of the object moving through the fluid. Derive a formula for dragging force of fluid by using dimensional analysis. (Hint: viscosity = ML-1T-1).
Solution
Given data
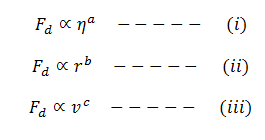
Required
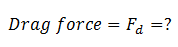
Strategy
We know the dimensions of force F on the LHS. As the dimensions in any valid physical equation are consistent, therefore, they must be equal to the dimensions on RHS. Using expressions (i), (ii) and (iii), we have to solve for the powers of dimensions on both sides.
Now from (i), (ii) and (iii),
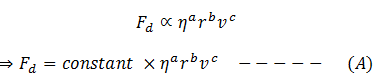
We know that the unit of force = newton = kg ms-2
Therefore, dimensions on LHS = [MLT-2] ——- (X)
Similarly, dimensions on RHS of equation (A) using (i), (ii), (iii)
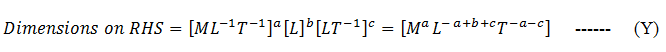
Equating the powers of dimensions M, L and T on both sides of (X) and (Y).
1 = a OR a = 1 ….. (1)
1 = -a+b+c OR -a+b+c = 1 . ….. (2)
-2 = -a-c OR a+c = 2 ….. (3)
From equation (1)
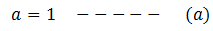
Put the value of ‘a’ from (a) in (3)
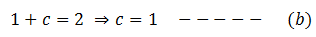
Put the values of ‘a’ and ‘c’ from equations (a) and (b) respectively, in equation (2),
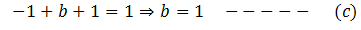
Now put the values of a = 1, b = 1 and c =1 from equations (a), (c) and (b) in equation (A).
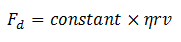
Experimentally determined value of ‘constant in this equation is 6π.
Therefore, formula for the drag force is
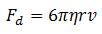
This is the required equation.

Pingback:numerical-problems-on-measurement-physics-11 – msa