A Carnot engine absorbs 2000 J of heat from the source of heat engine at 2270C = 500 K and rejects 1200 J of heat during each cycle to sink. Calculate efficiency of heat engine, temperature of sink and amount of work done during each cycle.
Solution
Theory: A Carnot heat engine operates between a hot reservoir and a cold (sink). It extracts some heat from the hot source, partly converts it to useful work and sends the rest to the sink.
In the given case, hot reservoir has a temperature of 2270C = (227+273) = 500 K. The temperature of the sink is not known, however, 1200 J of heat rejects to it in one cycle. The %efficiency of the engine is
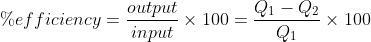
Since, Q is proportional to T, therefore, the above equation can also be written as
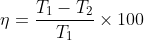
Calculation: Heat absorbed from the source, Q1 = 2000 J
Heat rejected to the sink, Q2 = 1200 J
Work done, W = Q1 – Q2 = 2000 – 1200 = 800 J
Now to find the temperature of the cold reservoir (sink) we find the efficiency of the engine by using equation (1) and then substituting for the efficiency in equation (2) to find the sink temperature. Thus
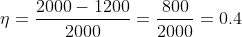
Put this value of efficiency in the above equation.
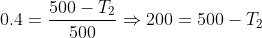
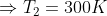
Note: In terms of centigrade scale, the temperature is 300 – 273 = 270C