Numerical Question 8: A 4.0 m long uniform ladder with weight of 120 N leans against a wall making 70° above a cement floor as shown in figure. Assuming the wall is frictionless, but the floor is not, determine the forces exerted on the ladder by the floor and by the wall.
Comprehension: Consider the diagram. The ladder is making an angle of 70° with the horizontal direction. Since the ladder is in equilibrium, the net force and torque is zero on the ladder. We consider the forces acting on the ladder.
- Its weight 120 N acting downwards at the center of the ladder. Since length of the ladder is 4 m and the ladder is uniform, therefore, the center of gravity lies at C at 2 m length.
- Force Fwall of the wall, acting horizontally towards left. Its magnitude is to be determined.
- Force exerted by the floor, F. It is also to be determined.
Construction: Resolve F, the force due to floor, into rectangular components Fx and Fy.
Solution
Since the ladder is in equilibrium, we apply the conditions of equilibrium, namely,
∑Fx = 0, ∑Fy = 0, ∑τ = 0
x-component of F and force by wall are two forces acting along the x-direction. Therefore,
y-component of F and weight of the ladder are two forces acting along the y-direction. Therefore,
Now consider point A as the point of rotation. Force of the wall produces an anticlockwise (positive) torque. The shortest distance between line of action of force and axis (at A) is AE = moment arm. Thus, 
is the magnitude of positive torque. Similarly, weight of the ladder produces a clockwise torque. The shortest distance between line of action of weight and axis (point A) is AD (moment arm). Thus 
is the clockwise (or positive) torque. Apply second condition, ∑τ is zero. We have,
But AD = AGcosθ (see the figure) and AG = L/2 and θ = 70°. This implies,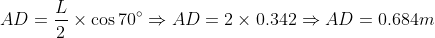 
.(Where L=4 m and cos70° = 0.342). Now consider the diagram. BC is the perpendicular in ΔABC and therefore, BC = ABsin70°. But AB = L = 4 m and sin70°= 0.939. Thus, BC = 4 × 0.939 = 3.756 m. Looking at the diagram, BC = AE, so put the values of AD, W and AE in equation (3),
This gives the force the wall exerts on the ladder.
This also gives the x-component of the force exerted by the floor on the ladder (equation 1). So, use equations (1) and (2) to find the magnitude of the force F by the floor.
This gives the force exerted by the floor. In order to find the direction of this force,
This gives the direction of the force by the floor.
Pingback:Numerical Problem 9, Vectors and Equilibrium … msa
Pingback:Numerical Problem 7, Vectors and Equilibrium … msa
Pingback:Numerical Problems on Vectors and equilibrium … msa