Problem 16: Two parallel plate capacitors A and B having capacitance of 2 µF and 6 µF are charged separately to the same potential of 120 V. Now positive plate of A is connected to the negative plate of B and the negative plate of A is connected to the positive of B. Find the final charges on each capacitor.
Solution
First we calculate the charge on each capacitor when they are charged separately.
Let Q1 is the charge on the first capacitor and Q2 on the second, then
Q1 = C1V which implies, Q1 = 2 × 120 = 240 μF … (1)
Q2 = C2V which implies, Q2 = 6 × 120 = 720 μF … (2)
Now the capacitors are connected as follow;
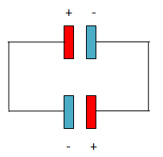
Now difference in charges on the capacitors = (720 × 10-6 – 240 ×10-6) = 480× 10-6 C
This charge will adjust on the capacitors according to their capacitances. To find the charge, we should know about the voltage across the capacitors.
Now, equivalent capacitance, Ce = CA + CB = 2μ + 6μ = 8 × 10-6 F
Voltage, V = Q/Ce = (480 × 10-6)/(8 × 10-6) = 60 V
Therefore, charge on capacitor A = 2 × 10-6 × 60 = 120 × 10-6 = 120 μF
Charge on capacitor B = 6 × 10-6 × 60 = 360 × 10-6 = 360 μF

Pingback:Numerical Problem 17, Electrostatics, Physics 12 – msa
Pingback:numerical-problem-15-electrostatics-chapter-2-physics-12-msa – msa
Pingback:numerical-problems-on-electrostatics-chapter-1-physics-12-msa