Question 5: Write note on pair production and annihilation of matter.

ANSWER

Pair Production

 It is the process in which energy is converted into two particles of matter. Sometimes, it is also called ‘materialization of energy’.

Explanation

When a high energy photon passes by a heavy nucleus or collide with the nucleus, the nucleus tries to stop it. This makes the photon disintegrated and converted into two particles. One of these particles is an electron and the other is a particle of mass equal to the mass of electron but having a unit positive charge. This particle is called positron. Both electron and positron move in opposite directions with the same speed.

Mass, energy, charge and momentum are all conserved in this process. Since the rest mass energy of an electron is m₀c² and the rest mass energy of a positron is also m₀c², therefore, total rest mass energy of the pair is m₀c² + m₀c² = 2m₀c². Therefore, pair production will happen only when the minimum energy of the incident photon is 2m₀c². In case the energy of photon is greater than this amount, the extra energy is transferred to the pair as its kinetic energy.

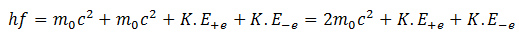
Since 2m₀c² = 2 * 0.51 = 1.02 Mev, therefore,

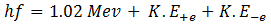
 So pair production will not happen if the energy of photon is less than 2m₀c². Hence 1.02 Mev is the minimum energy of photon required for pair production.

Annihilation of matter

Pair annihilation is the reverse process of pair production. An electron-positron pair produces two photons and annihilates in the process.

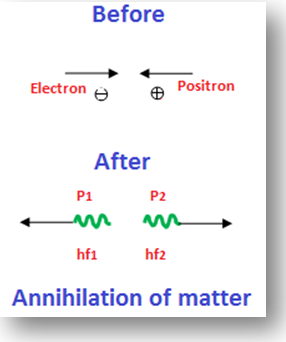
Consider the figure. An electron-positron pair annihilates to form two photons of energy hf₁ and hf₂. The sum of the energies of the photons must be equal to the total energy of the electron-positron pair.

Since the K.E of the pair is negligible as compared to their rest energies, so we assume they are at rest. Their total energy is m₀c² + m₀c² = 2m₀c² and total momentum is zero.  Now the two photons created must have energy = hf = m₀c² moving in opposite directions.

Pair production and pair annihilation confirms Einstein’s idea about mass and rest energy.