Question: Derive a relation between linear and angular velocities.
ANSWER

Let a particle is moving along a circle. If the initial position of the particle is at A and after a small interval of time ∆t, it reaches point B describing angle ∆θ. The linear displacement is equal to the length of arc AB = ∆s.
∆s is resulted due to the linear velocity of the particle which is along the tangent to the circumference of the circle. We know that ∆s = r ∆θ. Dividing both sides by ∆t,
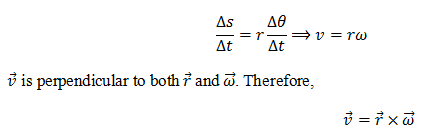

Pingback:angular-motion-different-parameters-of-angular-motion – msa