Question: What is simple pendulum? Diagramically show the forces acting on a simple pendulum. Show that a simple pendulum executes Simple Harmonic Motion.
Answer
Simple Pendulum
A simple pendulum is an ideal device which consists of a point mass suspended by a weightless, in-extendable string from a fixed frictionless support.
- It executes a periodic oscillatory motion in a vertical plane.
- Gravitational force or weight of the bob drives the motion.
- If the angle is small, the simple pendulum executes simple harmonic motion.
What is a point mass?
A point mass is an assumption that all the mass of the object is concentrated at a single point.
Consider the figure to the right.
- Point P is the mean position of the pendulum.
- Point O is the suspension point called pivot.
- A is the extreme position on one side. When released from A and there is no force of friction at pivot O and air drag on the way, it will reach the extreme position B on the other side.
- During the motion, its distance from the mean position P at any instant of time is called displacement, x.
- Maximum displacement is at A or B and it is called amplitude.
How a real pendulum can be approximated as a simple pendulum?
A real pendulum can be approximated as a simple pendulum if;
- Diameter of the bob is very small as compared to the length ‘l’ of the string.
- Mass of the bob is very large as compared to the mass of the string.
- The string is inextensible.
Force diagram of a simple pendulum
Consider the figure. The bob of the pendulum in on the extreme position Q. When released, it will move towards the mean position P.
There are two forces acting on the pendulum at Q; one the weight W = mg of the bob and the other tension T in the string. But the bob doesn’t move in the direction of any of these forces. Therefore, some component of these forces is responsible for the motion of the bob. Let it is weight W. Thus resolve W into rectangular components one along the line of tension T.
From the figure,
The y-component of W is the force which is responsible for the motion of the pendulum.
To show the motion of simple pendulum is simple harmonic motion
The x-component mgcosθ is opposite to the tension T in the string. Since there is no motion along any directions of T, therefore, mgcosθ must be equal to T and will be cancelling one another.
The y-component has the same direction as that of the motion of the pendulum. Therefore, this must be causing the motion of the pendulum. Therefore, the restoring force which drives the pendulum is,
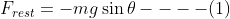
Now, weight W is parallel to OP and T and mgcosθ are collinear, therefore,
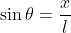
Put this value in equation (1),
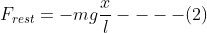
Now m, g and ℓ are constants, therefore,
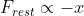
This is condition for Simple Harmonic Motion. Therefore, if the displacement is small, the motion of a simple pendulum is simple harmonic one.
Similarly, by Newton’s Second Law
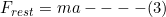
Compare equation (3) with equation (2),
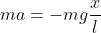
Simplify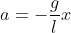 
Now g and ℓ are also constants, therefore,
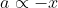
This acceleration is caused by the component mgsinθ of the weight W of the bob and shows the motion of the pendulum is simple harmonic motion.