Question 2: State and explain Stokes’s Law? Derive a mathematical equation for terminal velocity by using Stokes’s Law.
ANSWER
Stokes Law
When an object is moving through a fluid, it experiences a retarding force called the drag force. When the speed of the object increases, the drag force also increases and vice versa. This force is in fact resistance offered by the fluid to the moving object and called viscous drag.
The viscous drag depends upon the size, shape, orientation and the relative speed of the object.
Stoke mathematically calculated the drag force acting on a spherical body moving in a fluid, called Stokes’s Law.
FD = 6πηrv … (1)
Where FD = Drag force
η is the coefficient of viscosity of the fluid
‘r’ is the radius of the spherical object moving through the fluid
‘v’ is the velocity of the object.
Terminal Velocity
Terminal velocity is the maximum constant velocity attained by a freely falling body in a viscous medium.
Stokes’ law is used to calculate the terminal velocity of a spherical body falling freely in a viscous medium.
Consider a spherical water drop falling freely due to the action of gravity. Let at point ‘A’ it is just starting to fall. The force acting on the drop is its weight. At the same time, when it starts to fall down, it starts experiencing the resistance or drag force by the medium (say air). Now under the force of gravity, the velocity will be increasing as the drop falls down as the gravitational force continuously attracts it. At the same time, the drag force or resistance of the air will also be increasing. As the drop falls faster, the resistance also increases. A stage will reach when the drag force will become equal to the weight (gravitational force) of the drop. The net force on the drop will be zero now. However, reaching this stage, the drop would have attained some velocity and now it will be falling down with this velocity steadily. This velocity is called Terminal Velocity.
Now under these conditions, FD = mg
Therefore,
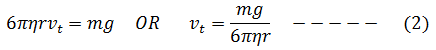
(vt) being the terminal velocity.
If V is the volume of the spherical droplet, then mass density = ρ = m/v ⇒ m = ρV
Volume of a sphere is given by,
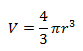
Put this value for volume of the drop in the above equation (m = ρV),
![]()
Now put this value in equation (2).
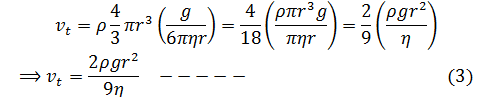
This equation shows that vt ∝ r2, since the remaining part on RHS of this equation is constant.
Since terminal velocity is proportional to the square of the radius of the body, therefore, if two masses of the same density (mass per unit volume) are allowed to fall down in a viscous medium the lighter mass will attain terminal speed first than the heavier one.

Pingback:index-lq-ch6-p11 – msa