Question 2: Both Zarak and Samina are twenty years old. Zarak leaves earth in a spacecraft moving at 0.8 c while Samina remains on the earth. Zarak returns from a trip to a star 30 light years from the earth.Which one will be of greater age?

ANSWER

We suggest you read this Urdu article on twin paradox first.

According to special theory of relativity, a clock traveling at a high speed appears to run slowly. Similarly, the length contracts (shortens) when we are concerned with the speeds comparable with the speed of light.

In the given problem, Samina would be older than Zarak when he returns from his trip to the star at a 30 light years distance. It is because time will pass slowly on the spacecraft. All processes that depend on time will also occur slowly including the age of a human beings.

The present ages of both are 20 years. When Zarak sets off for his round trip journey (going and coming back), to the star at 30 light years distance (and 30 light years is distance not the time! Try to calculate that one light year is equal to 94608 ×  10¹¹ m), his age can be calculated by the time he takes to complete his round trip. S = vt  OR    t = S/v   …   (1)

In this case, distance S = 2 × 30 = 60 light years.

However, in meters the distance is, S = 60 × 94608 × 10¹¹ m

And velocity of the spaceship, v = 0.8 c

Therefore, put for S and v in equation (1) to find time t,

(from earth point of view) = 20 + 75 = 95 years.

On the other hand, time will pass slowly in the spacecraft. 75 years on the earth will be less on the spacecraft according to the relativistic time dilation,

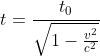
Put values as t = 75 years, v = 0.8c and t₀ as the time in the spacecraft (age of Zarak).

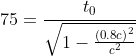
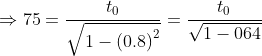
Hence, Zarak will be (45 + 20 =) 65 years old when he returns from his journey and will be (95-65 =) 30 years younger than Samina.

(We suggest you try to find the age of Zarak by one another method. Find the contracted length by applying the formula of length contraction. Then apply formula t = S/v and find the time passed in the spaceship. It also gives the same result, i-e, 45 years. Otherwise you can see it here.).