Question 11: Explain the vibration in a closed organ pipe. Show that the frequency of third harmonic is 5v/4L .
ANSWER
A pipe whose end opposite to the whistle end is closed is called a closed organ pipe.
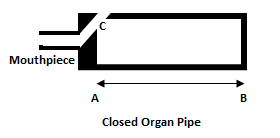
In the diagram a closed organ pipe is shown. It consists of a hollow tube AB = L in which air can be blown through a mouthpiece. There is a sharp edge C at the open end of the pipe which is called ‘lip’. (In our local musical instruments, we call it ‘tongue, i-e, jaba‘). The lip sets up vibration in the air column enclosed into the closed organ pipe.
Now when a narrow jet of air is sent toward the lip through the mouthpiece this air strikes the lip under pressure. It sends a compression into the pipe. The compression when reaches the closed end is reflected back toward the open end. At the lip this compression pushes the air outside the lip and a rarefaction is sent into the pipe. Reaching the closed end, the rarefaction is reflected and when it reaches the open end, it draws air into the pipe. Thus another compression is produced and the process is repeated.
Now from first compression to the formation of the second compression the air travels the pipe 4 times (1: First compression goes and strikes the closed end.2: The compression returns from the closed end toward the open end. 3: Rarefaction goes toward the closed end. 4: Rarefaction goes toward the open end. New compression goes toward the closed end after these 4 journeys of the pipe). We know that the distance between one compression to another is equal to wavelength of the wave. Therefore, the full length of the pipe is one-fourth of the wave length, i-e, L = λ/4.
To show that in third harmonic, f = 5v/4L

In order to find the frequency in the third harmonic, we suppose,
Velocity of the sound = v
Wavelength of the sound = λ
Frequency of the sound = f
Length of the closed organ pipe = L
Also we know that 2 loops = 1 wavelength = λ
Now consider the diagram on the right. The air column in this case must vibrate in two and a half loops. Now it is clear from the figure that,

Now we know that, v = fλ ⇒ λ = v/f.
Put this value in equation (1)
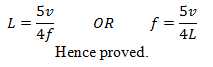

Pingback:index-cqs8-p11 – msa
Pingback:Comprehensive Questions on Waves … msa – msa
Pingback:organ-pipes-and-harmonics – msa