Question 12: Explain why we can experimentally observe the wave-like properties of electron but not of a billiard ball?

ANSWER

 de’ Broglie wavelength associated with a moving particle is given by

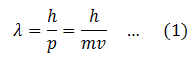
So the wavelength of a moving particle depends upon the mass and velocity of the particle. This equation for the wavelength of the matter wave explains why the wavelength of large particles is not observable.

(1) In the case of an electron, mass of the particle (i-e, electron) is very very small. When the mass of the particle is small, its wavelength should be larger (equation 1). In case of electron, it is of the order of few angstroms. This wavelength is comparable to the distance between the atoms of a crystal, and hence, suitable for studying for certain wave characteristics like diffraction and interference. Therefore, the wave-like characteristics of the motion like diffraction and interference of an electron can be detected.

(2) For larger masses like billiard ball, the wavelength is consequently so small that it cannot be detected (equation 1) by any instrument. Therefore, we cannot observe the wavelength of larger bodies like a billiard ball.

Follow up example

(1) Take the mass of electron as 9.1 × 10^-31 kg and speed v = 1 × 10⁶ m/s and apply equation (1) to find its wavelength. You will see it is of the order of few A°. This will be comparable with spacing of atoms in some crystals and hence can be studied for diffraction.

(2) Take a billiard ball of mass 0.25 kg moving with a velocity of 20 m/s. Apply equation (1) to find its wavelength. It will be extremely small to be studied for the wave characteristics like diffraction or reflection. Hence, we cannot observe the wave-characteristics of a billiard ball.

Note: Value of h = 6.63 × 10^-34 m²kg/s.