Question 13: Compare the formula for capacitors in series and parallel with those for resistors in series and parallel.

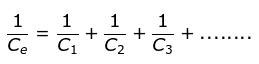
ANSWER

A: When more than one capacitor is connected in series, the reciprocal of the equivalent capacitance C_e of the individual capacitors is equal to the sum of the reciprocals of the capacitors.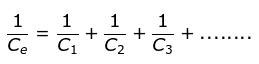

When more than one resistor is connected in series, the equivalent resistance R_e is equal to the sum of the individual resistances. R_e = R₁ + R₂ + R₃ +……….

B: When many capacitors are connected in parallel, the equivalent capacitance C_e is equal to the sum of the individual capacitances of the capacitors.
C_e = C₁ + C₂ + C₃ +………..
When many resistors are connected in parallel, the reciprocal of the equivalent resistance is equal to the sum of the reciprocal resistances of the individual resistors.
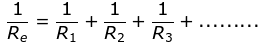
We can easily see the patterns are different in both cases.

Explanation

In the series combination case the equivalent capacitance of the capacitors become smaller than the individual capacitors. However, when resistors are connected in series, their equivalent resistance is larger than the resistances of the individual resistors. In the parallel combination case the equivalent capacitance of the combination of capacitors is greater. On the other hand, the equivalent resistance of the resistors decreases in the case of parallel combination.