Problem 1: An object travels 60 m in the first 6 seconds. Then keeps uniform motion for next 9 seconds. In the last 10 seconds of the journey it de-accelerates uniformly to rest. Find:
(i) maximum speed attained in the journey (ii) total distance traveled in the
(ii) total distance traveled in the whole journey.
Solution
Strategy: The journey of the object can be divided in three parts; first it accelerates for 6 seconds from rest, second travels for 9 seconds with uniform velocity and finally, decelerates to rest again. The final velocity in the first part of journey is the initial velocity for the second part and final velocity in the second part of the journey is the initial velocity for the third part. However, the object travels with uniform velocity in the second part; therefore, the same velocity is the initial velocity at the start of third part as well.
Moreover, we have to find the speed of the object in all these three parts and to see where the object attains its maximum speed. Also we have to calculate the distances covered in the three parts and sum them up to find the total distance covered during the course of journey.
First part of the journey
Vi = 0 m/s t = 6 sec s = 60 m Vf =?
However, to find final velocity, we have to find the acceleration first.
Apply second equation of motion,
S = Vit + ½ at2
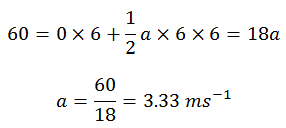
So final velocity is
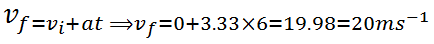
Second part of the journey
Vi = 20 ms-1 t = 9 sec S = ?
Apply formula S = vt, we have
S = 20 × 9 = 180 m
Third part of the journey
Vi = 20 ms-1 Vf = 0 ms-1 t = 10 sec S =?
But we have to find the deceleration first. Apply first equation of motion
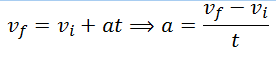
Put the values
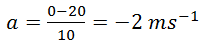
Apply third equation of motion to find distance
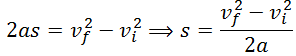
Put the values
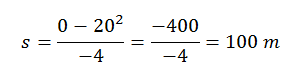
Take a glance of the data in all the three parts. We see
Maximum speed attained during the whole journey = 20 m/s
Total journey = 60 + 180 + 100 = 340 m
Question or feedback? Text on 03488519873

Pingback:numerical-problems-force-and-motion-chapter-3-physics-11