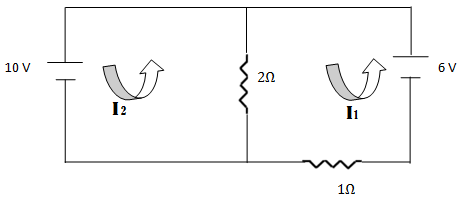
Problem 8: Find the current flowing through the resistors of the fig.

Solution

We apply KVL to solve this problem. (Remember the problem is too complicated for Ohm’s law as this consists of multiple emf sources).

We take two loops in the circuit in which currents I₁ and I₂ are flowing. Take the first loop with current I₁ and start from the battery 6 V and going anticlockwise with the current.

1. We go to the positive terminal, up in the potential, so the voltage is taken positive, +6.
2. We reach the middle resistance of 2 ohms where two currents are flowing in this resistor. As we are going along the current (towards a point at lower potential as current always go to the lower potential), therefore, the potential drop is negative. Similarly, current I₂ is coming from the other side therefore, the voltage drop in this resistance is – (I₁– I₂) R₁.
3. In the second resistance on the way, we go along the current, that is, from higher to lower potential. Therefore, voltage drop is –I₁R₂. And we reach the same point where we had started.

Therefore,

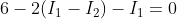
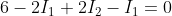
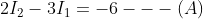
Now consider the other loop with current I₂. Start your tour from the emf source of 10 V along the direction of current in the loop.

1. At the emf source, we go from high potential to low potential, hence, emf is -10.
2. The potential drop at the resistor of 2 Ω  is –2(I₂-I₁).

Therefore, the equation for this loop is

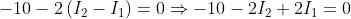
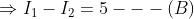
Multiply (B) with 2 and add with (A)

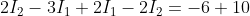
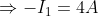
 Negative sign shows the assumed anti-clockwise direction of this current is not correct. Therefore, I₁ = 4 A in the clockwise direction.

Put this value in (B)

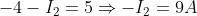
Again the negative sign indicates the current flow in the clockwise direction.