Question 4: Explain the terms mass defect and binding energy related to a nucleus.

ANSWER

Binding Energy

It is defined as the work done needed to separate a nucleus into separate protons and neutrons.

We know that the potential energy is due to the relative position of the particle in the system. A high potential energy means the particle is not at the place where it tends to be. The place where the particle tends to be in a system is the state of lowest energy. Now the protons and neutrons  in a nucleus are held together by a strong attractive force. This force prevents protons to push away from one another. If we want to separate the protons and neutrons from one another we must do work to overcome this force. This work done is called as binding energy.

Binding energy per nucleon (nucleon means a single proton or a single neutron) of a nucleus is the binding energy divided by the number of nucleons.

Mass defect

The mass of a nucleus is less than the mass of the same number of individual protons and neutrons put together. This difference in masses is called mass defect of the nucleus. So mass defect is defined as

“the decrease in the mass during the formation of a heavy nucleus is called mass defect.”

Mass defect is due to the binding energy of the nucleus and binding energy of the nucleus can be calculated from the mass defect. Using Einstein’s mass-energy equation,

Binding energy = mass defect * c²          …          (A)

Mass defect can be calculated as follow,

Let _ZX^A is any nucleus having mass A. The mass defect, in amus, of the nucleus is

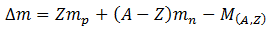
Where m_p is the mass of a proton, m_n is the mass of a neutron, Z is the number of protons, (A-Z) is the number of neutron and M_(A,Z) is the mass of the nucleus. Thus using equation (A), binding energy can be calculated. Find that we will be able to find energy per nucleon, as well.