Question 2: What are Bohr’s postulates about Hydrogen atom? Hence derive expressions for (i) radii of electron orbit (ii) energy of the electron.
ANSWER
Neil Bohr proposed a theory of the Hydrogen atom based on the ideas from classical Physics, Plank’s Quantum theory and Einstein Photon theory of light. His model consists of the following postulates.
(1) Electron revolves around the nucleus under the influence of the electrostatic force between the electron and nucleus.
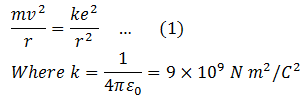
(2) Electron cannot revolve the around the nucleus in any arbitrary orbits. Only those orbits are allowed for which the orbital angular momentum is an integral multiple of (h/2π). Therefore,
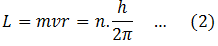
For n = 1, 2, 3…
(3) The electron in the stable orbits (allowed orbits) does not radiate any energy as in the classical theory. Its energy remains the same as far as it is in the specific orbit.
(4) When an electron jumps from higher energy orbit to a lower energy orbit an electromagnetic radiation of frequency f is emitted.
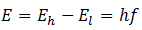
Radii of electron orbit
The electrostatic force F between electron and proton, both having the same charge e is,
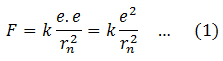
This force provides the necessary centripetal force for the electron to revolve around the nucleus.
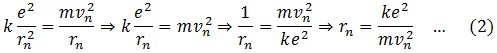
From Bohr’s second postulate
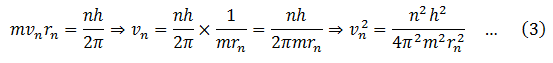
Put this value of vn in equation (2).
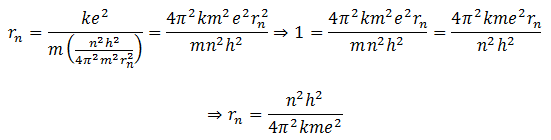
We can solve this equation for rn by putting the values. It is found that rn = n2.0.53 A0. Therefore, when n =1, the radius of the first orbit = 0.53 A0. Similarly, for n=2, r2=4*0.53 = 4r1, for n=3, r3=9*0.53 = 9r1 and so on.
Energy of the electron
Total energy of the electron in a certain orbit n is the sum of its kinetic energy and potential energy. Therefore,
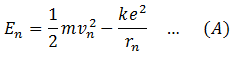
To calculate the K.E of the electron, apply Bohr’s postulate that the electrostatic force between the electron and nucleus is equal to centripetal force.
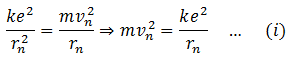
Put this value in (A)
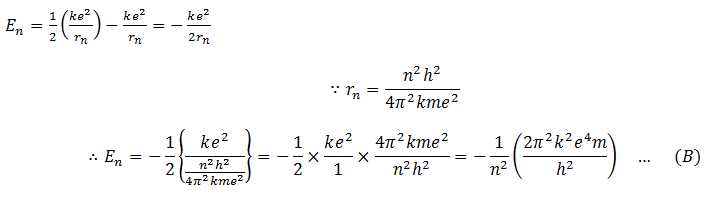
For n = 1
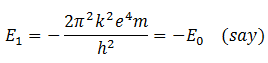
Then in light of equation (B) the energy of electron in any orbit n is,
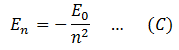
And can be calculated by substituting the value of E0. Numerically, E0 = 13.6 therefore, En = (-13.6/n2) ev. The negative sign shows the electron is bound to the nucleus and cannot escape.
Frequency Calculations
We know that En = hfn OR fn = En/h.
Put the value of En from equation (C)
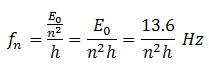

Pingback:excitation-energy-ionization-energy-normal-state-excited-state – msa
Pingback:spectrum-of-hydrogen – msa
Pingback:mcqs-atomic-spectra-p-12 – msa
Pingback:long-questions-ch19-p12