Consider a parallel plate’s capacitor with comparatively large plates each of area A with a small separation d. In such a case electric field intensity is uniform between the plates and fringing are negligible. Let the medium between the plates is vacuum or air. Now suppose the capacitor is charged to an amount of charge Q; therefore, the surface charge density (charge per unit area) is

 Let the potential difference between the plates is V. Using Gauss Law

and put the value of σ, the electric intensity between the plates is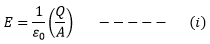 Now using the following equations; 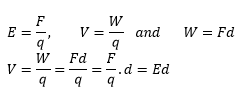Put the value of E from equation (1) 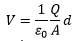We know that capacitance of a capacitor is C = Q/V. Therefore, put the value of V (from the above) in this equation.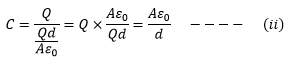 Capacitance when dielectric is inserted Let a dielectric of relative permittivity ε_r is inserted between the plates of the capacitor. Then the capacitance of the capacitor increases by a factor ε_r. This equation shows that the capacitance depends upon the area of the plates A, their separation d and medium between them. Larger plates, closer they are and higher the dielectric constant of the medium between the plates, the greater will be the capacitance of the capacitor. Now let’s divide (iii) by (ii),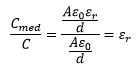 The relative permittivity is the ratio of the capacitance’s of a capacitor with a given material filling the space between the two plates to the capacitance of the same capacitor when the space is evacuated. This is also called dielectric constant or specific inductive capacity.