Question 2: Explain the diffraction of X-rays by crystal and derive an expression for Bragg’s Law to find the wavelength of light used.
ANSWER
One of the useful applications of interference and diffraction is the study of the structure of crystals in matter. However, it was difficult in practice because the layers of atoms in the crystals are very close to one another, in fact, less than one nano meter (10-9 m). Hence to study such structures, it was necessary to use radiations having a wavelength of the same order (10-9 )m.
Since X-rays have a very short wavelength, of comparable range, but its interference fringes were impossible to obtain by Young’s Double Slit arrangement or thin films. Because in order to have such interference fringes we need slits separated by at least 10-10 m. This is so small that we can’t have them in Young’s experimental apparatus. However, X-rays diffraction was possible using NaCl crystal. In such a crystal, the spaces among the atoms are uniform and of the order comparable to the wavelength of X-rays.
Experiment
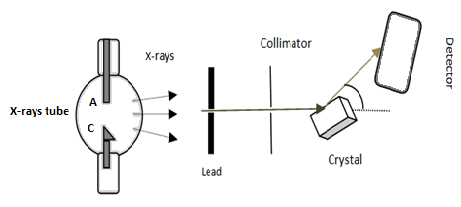
A narrow beam of X-rays from some X-ray source is passed through a collimator and allowed to fall on the crystal. The transmitted beam then enters the detector D. (See fig). The Laue photograph thus obtained consists of a central spot surrounded by many other spots in a definite pattern. These spots are called Laue spots. It is different for different crystals due to different intra-atomic arrangements of crystals.
It proves that;
(1)X-rays are electromagnetic radiations of a very short wavelength.
(2)Atoms of the crystals are arranged in 3-dimensional lattices.
Bragg’s Law
Bragg’s Law is used for finding the wavelength of X-rays.
The law states that constructive interference takes place when the difference in the path length BCB’ is equal to an integral number of wavelength; 2dsinθ = mλ.
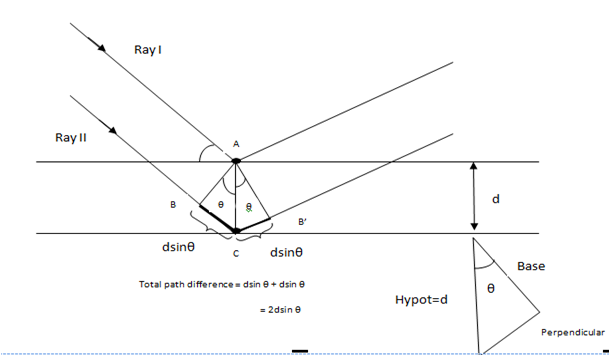
Consider the diagram. Two parallel rays I and II are incident on the first and second layers of the crystal. Separation between the two layers is ‘d’ and θ (called the Bragg’s angle) is the angle of incidence. Now, ray I is reflected from A (think about an atom present at point A which reflects the ray) and ray II is reflected from C (again there must be an atom at C which reflects the ray). Now we see from the figure that ray II covers more distance than ray I. The total increase in the path for ray II is BC + CB’.
To calculate the path difference mathematically, we see,
path difference = BC + CB’ = dsinθ + dsinθ = 2dsinθ
So, for the constructive interference to happen, the path difference should be integral multiple of the wavelength, λ.
Path difference = 2dsinθ = mλ
Where m = 0, 1, 2, 3… …
This equation represents Bragg’s Law. Knowing the value of λ, we can find the inter-planer spacing of the planes of the crystal.
X-rays diffraction is very useful in finding the structure of biologically important molecules such as hemoglobin and double helix structure of DNA.

Pingback:interference-fringes-fringe-spacing – msa
Pingback:dual-nature-of-light – msa
Pingback:Comprehensive Questions, Physical Optics … msa – msa
Pingback:Physical Optics, Comprehensive Questions … msa – msa
Pingback:index-cq-ch9-p11