Question 4: Explain the terms: emf, internal resistance and terminal potential difference of a battery.
ANSWER
Electromotive force (emf)
The energy per unit charge supplied by a source to move the charge from the negative terminal to the positive terminal of the source (from lower to higher potential) is called the emf of the source.
To maintain a steady current in the conductor, a steady potential difference across the conductor should be applied. This is possible only when some device changes some other form of energy into electrical energy; car battery converts chemical energy into electrical energy as an example. “A device which converts non-electrical energy into electrical energy is called a source of electromotive force”.
The source does work on the charge entering its negative terminal, driving it up the potential gradient, through itself. At higher potential point, i-e, positive terminal, it gains energy W. This energy is equal to the work done on the charge by the source and called emf of the source, denoted by ε.
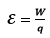
Emf and PD are measured in the same units, volt ( joule/coulomb); however, emf is a special kind of PD which arises through the transformation of some other form of energy to electrical energy.
emf sources
- Electrical cells or batteries convert chemical energy into electrical energy.
- Electric generator converts mechanical energy into electrical energy.
- Solar cells convert light energy into electrical energy.
- Thermocouples convert heat energy into electrical energy.
Internal Resistance
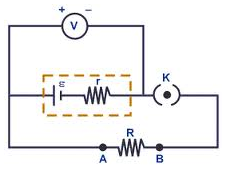
The terminal voltage, Vt, of a battery when it delivers a current I is equal to the total emf minus the voltage drop in internal resistance r. When no current is delivered then Vt is equal to the emf of the battery.
Relation between emf, internal resistance and terminal potential
Suppose a load resistor is connected across an emf source ε then the equivalent resistance Req is R + r (resistances in series). Applying Ohm’s Law,
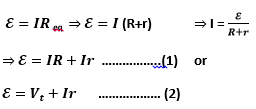
Where Vt = IR is the terminal voltage of the battery.
This equation represents a relation among terminal voltage, emf and internal resistance.
Vt can be calculated from this equation as, Vt =ε-Ir
Energy interpretation
Consider equation 1. The left side of the equation is the energy gained by a unit charge as it goes through the battery. The right side gives an account of the utilization of that energy; part of the energy gained (Ir), is dissipated into the battery and the rest, IR, in the external circuit. Thus the emf supplies energy to the charge as source of energy and the potential drop across various elements dissipate this energy into other forms of energy.

Pingback:construction-of-rheostat-and-its-uses – msa
Pingback:ohms-law-scope-and-validity – msa
Pingback:Comprehensive Questions, Current Electricity … msa – msa