Question 1: (a) Sketch the graph of emf induced in an inductive coil against rate of change of current. What is the significance of the gradient?
(b) Explain why it is difficult to measure the rate of change of current?
(c) How do graph of emf against time and current against time make it possible to measure self-inductance?
ANSWER
(a) When an alternating current is flowing through an inductor, or the amount of current flowing through the inductor changes, an emf is induced in the inductor. It is found that the emf and change in the current are directly proportional to one another. If ΔI is the change in the current in time Δt, rate of change of current is ΔI/Δt. Let ϵ is the emf produced in the coil, then
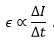
Therefore, the graph sketch of the rate of change of current and the induced emf is a straight line.
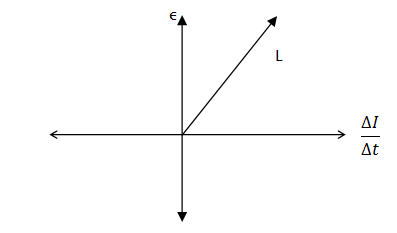
Significance of the gradient of the graph
When graph is plotted between two quantities, its gradient shows how one quantity (on y-axis or dependent quantity) changes when a change is brought in the other quantity (on x-axis or independent quantity). Mathematically,
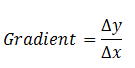
In case of rate of change of current and induce emf in the inductor, the gradient is
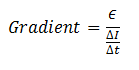
Now consider the proportionality of induced emf and rate of change of current in the conductor,
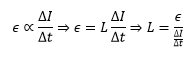
Therefore, by comparison,
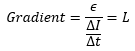
Now if the gradient of the graph is greater, this means a larger change in the emf is induced with a small rate of change of current. When a small current change in some time interval induces more electromotive force ϵ, the inductance of the inductor has a larger value.
When the gradient of the graph is small, this means a smaller emf induced in the inductor with a large rate of change of the current. Consequently, the inductance of the inductor is small.
Therefore, the importance of the gradient of the graph between emf and rate of change of current is that it shows the inductance of the inductor.
(b) An alternating current is continuously changing in magnitude as well as in direction. The change takes place many times in a second (usually 50 times per second). To find the change, we insert some current measuring meter like a galvanometer somewhere in the line of current. With the change in the current, the instrument also changes its direction from one side to another. The changes are so speedily happening that it becomes very difficult to measure the rate of change in it. So it is usually very difficult to measure the rate of change of an alternating current.
(c)When a sinusoidal current (that is current varying with time) is applied across an inductor, it induces an emf in the inductor. If ϵ is the induced emf and ΔI is change in the current in time interval Δt, then
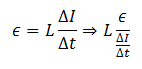
So the inductance of an inductor is the ratio between induced emf ϵ and current at a particular instant. Therefore, the inductance of an inductor can be easily calculated by finding the ratio (ratio is the quotient of the division) of induced emf and time rate of current. Inductance L of an inductor is more if the induced emf is more for a certain value of ΔI/Δt and vice versa. The value of change in the induced emf ϵ and time rate of current can be determined by the graph plotted between the two quantities. So this graph can be used to find the ratio of emf vs. rate of change of current which is the inductance L of the inductor.

Pingback:work-in-a-resistance-is-ve – msa
Pingback:sq-ch5-p12