Question 2: (a) Current and voltage provided by an AC generator are sometimes negative and sometimes positive.(a) Explain why for an A.C generator connected to a resistor power can never be negative?

(b) Explain using sketch graphs, why the frequency of variation of power in an AC generator is twice as that of the current and voltage?

ANSWER

(a) When a resistor of resistance R is connected across an A.C generator, the instantaneous sinusoidal voltage and instantaneous sinusoidal current is given by

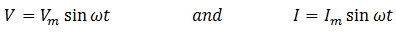
This means that both instantaneous voltage and instantaneous current are in phase. (You know ωt is the phase angle at any instant of time t and it is same for both current and voltage, therefore, both current and voltage are in phase) When the voltage is positive, current is also positive and when voltage is negative, current is negative. Now the power delivered to the circuit is

P = IV

This equation shows that power will always be positive. It is because when V is negative, I will also be negative. Therefore, when both I and V are negative, their product is positive and Power is positive. If both I and V are positive, their product, i-e, power is also positive.

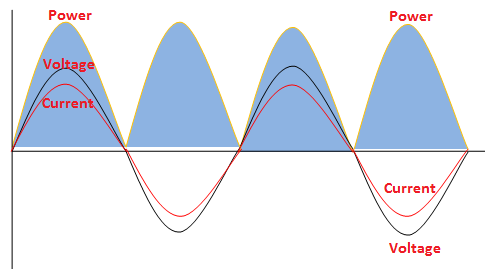
Since it is not possible at any instant of time that one quantity is positive and the other is negative, therefore, power will always be positive.

(b) Since power is always positive, therefore, it attains its maximum value twice during a cycle. We know that  

P = V_rmsI_rms

Now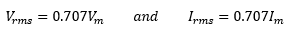

Put these values in equation (I)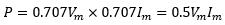

Multiply both sides by 2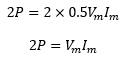

This means power varies sinusoidally at a frequency twice the frequency of either voltage or current.