Question 5: Calculate the escape velocity of a body and show that it is equal to 11.2 kms-1.
ANSWER
Calculation of escape velocity
From our daily life experience we know that when a body is projected up, it falls down after attaining a certain height. If the initial velocity of projection is increased, it goes to a higher distance above in the atmosphere. This indicates that if we increase the velocity of projection further and further, a stage will come when the body will go out of the influence of gravitational pull and will never come back!
The initial velocity which a projectile must have at the surface of earth in order to go out of earth’s gravitational field is called escape velocity.
In order to calculate the escape velocity, we know that the work done required to lift a body from earth’s surface to a far off distance where it is not influenced by the force of gravity is

 it will reach to an infinite distance and escape out of the gravitational field. So, if vesc is the escape velocity at earth’s surface, then
it will reach to an infinite distance and escape out of the gravitational field. So, if vesc is the escape velocity at earth’s surface, then
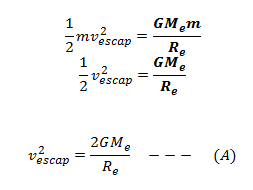 We know that,
We know that,
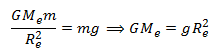 Put this value of GMe in equation (A),
Put this value of GMe in equation (A),
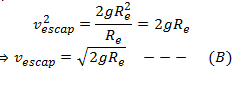 Equation (B) gives the initial velocity at earth’s surface that will enable the body to escape from the earth’s gravitational field and, hence, called escape velocity.
To show that escape velocity is equal to 11.2 km/s
We know that g = 9.8 m/s2
and Re = 6.4 x 106m.
Put these values in equation (B),
Equation (B) gives the initial velocity at earth’s surface that will enable the body to escape from the earth’s gravitational field and, hence, called escape velocity.
To show that escape velocity is equal to 11.2 km/s
We know that g = 9.8 m/s2
and Re = 6.4 x 106m.
Put these values in equation (B),
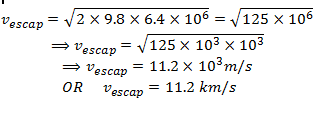
This proves the result.
Where m = mass of the object Me = mass of the earth G = Gravitational constant.
Hence, if a projectile is given an initial KE equal to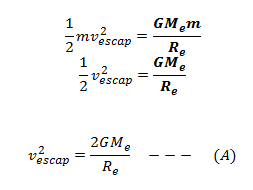 We know that,
We know that,
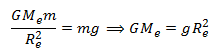 Put this value of GMe in equation (A),
Put this value of GMe in equation (A),
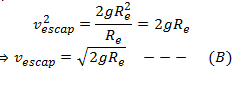 Equation (B) gives the initial velocity at earth’s surface that will enable the body to escape from the earth’s gravitational field and, hence, called escape velocity.
To show that escape velocity is equal to 11.2 km/s
We know that g = 9.8 m/s2
and Re = 6.4 x 106m.
Put these values in equation (B),
Equation (B) gives the initial velocity at earth’s surface that will enable the body to escape from the earth’s gravitational field and, hence, called escape velocity.
To show that escape velocity is equal to 11.2 km/s
We know that g = 9.8 m/s2
and Re = 6.4 x 106m.
Put these values in equation (B),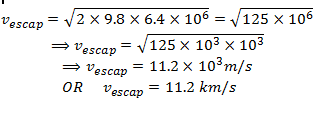
This proves the result.

Pingback:Work, Power and Energy, Comprehensive Questions