Question 2: Show that angular momentum in magnitude is given by

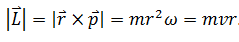
ANSWER

Torque produces or changes the rotation of a particle about an axis of rotation. This means torque produces angular acceleration α.

Torque is defined as the twisting (turning) force that tends to cause rotation.

Angular momentum is the quantity of motion of a body that is moving in a circle. Quantity of motion means how easy or difficult it is to stop the body from moving in the circle.

Physically, it is the cross product of moment arm 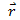  and force .

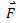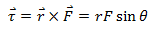
The angular momentum of this particle is;

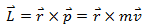
Here 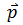   is the linear momentum of the particle.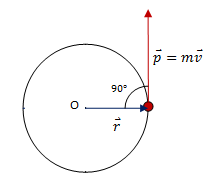

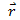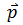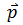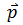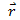Consider a body in motion in a circular path as shown in the figure.    is perpendicular to   at any point of the circular path. Therefore, momentum   is tangential to the circle. The angle between   and   is 90° and hence,

L = rpsin90° = rp

Now p = mv    and     v = rω

Therefore, in terms of magnitudes,

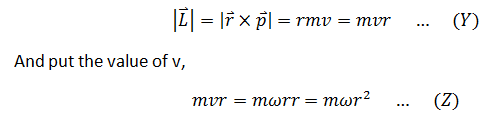
Equations (Y) and (Z) prove the result.