Question 1: Find the average rate of change of the following functions over the indicated intervals:
Solution
a. y = x2 + 4, from x = 2 to x = 3
Put the values,
Simplifying,
OR
Now the given interval is from x = 2 to x = 3. This means
Δx = 3 – 2 = 1
Put this value in the above equation
Δy/Δx = 2(2) + 1 = 4 + 1 = 5 Answer.
b. y = x2 + 1/3 x<, from x = -3 to x = 3
Let y = f(x) = x2 + 1/3 x
The rate of change is given by
Put the values then
Now multiplying the numerator and denominator by 3 and cancelling the concerned terms
Cancelling Δx,
Since the given interval is from -3 to +3, i-e, 6 units in the positive direction, therefore, Δx = 6. Put values
c. S = 2t3 – 5t +7
Let S = f(t) = 2t3 – 5t +7 then
f(t + Δt) = 2(t + Δt)3 – 5(t + Δt) + 7
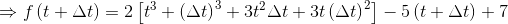
Therefore, rate of change is
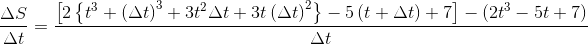
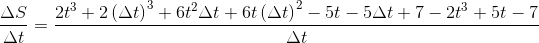
Cancelling similar terms with opposite signs,
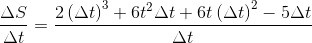
Taking Δt common in the numerator and cancelling it with the denominator, we get,
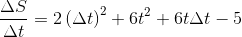
Since the given interval is from t = 1 to t = 3, therefore, Δt = 3 – 1 = 2. Therefore,
d. 
from t = 8 to t = 8.5
Let
Then
And the rate of change of h is
Now from the given data, t = 8 and Δt = 0.5, therefore,
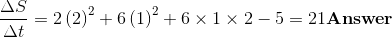
Pingback:Math’s 12, Exercise 2.1