
Select the correct answer of the following questions:
1. A three meter tall cylinder, full of water, has four identical small holes at heights 2.1 m, 2.2 m, 2.3 m and 2.4 meter. The speed of afflux is maximum from
| (a) 2.1 m high hole | (b) 2.4 m high hole | (c) 2.3 m high hole | (d) 2.2 m high hole |
Hint: 2.1 m high hole is the lowest of all.
2. A raindrop of radius ‘r’ falls in air with a terminal speed vt. What is the terminal speed of a rain drop of radius 2r?

Solution
Since both the rain drops have similar mass density, therefore, we apply the equation for terminal velocity in terms of density.
When the radius of the droplet is ‘r’
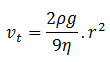
When the radius of the droplet is 2r,
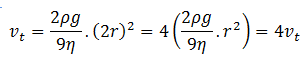
3. Eight spherical drops of same mass and radius are falling down with a terminal velocity of 6 cms-1. If they coalesce (combine together) to form one big drop, what will be its terminal speed? Neglect buoyancy due to air.
| (a) 1.5 cm s-1 | (b) 6 cm s-1 | (c) 24 cm s-1 | (d) 32 cm s-1 |
Solution
When 8 drops of same masses and densities combine together to form a single drop then the mass and volume of the single drop is 8 times larger than the mass and volume of the individual drops. Let m and V are the mass and volume of each individual drop and m’ and V’ are the mass and volume of the single drop after combining with one another.
8m = m’ and 8V = V’
Now in terms of radius, volume is given by
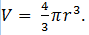
Therefore,
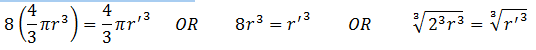
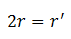
Now to find the terminal velocity of the big drop, we use the formula
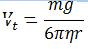
Therefore,
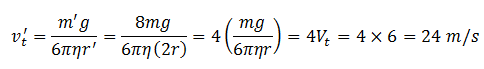
4. Water flows steadily through a horizontal pipe of variable cross-section. Find the pressure at another point where the velocity of fluid flow is 2v. Consider ρ as density of water.

Solution
Bernoulli’s theorem states,
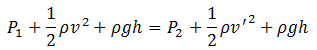
Since the pipe is horizontally laid, its height is same throughout the length of the pipe; therefore, the term ρgh is same on both sides.
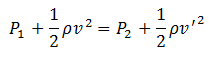

5. The cylindrical tube of a spray pump has a radius R, one end of which has ‘n’ number of fine uniform holes, each of radius ‘r ‘. If the speed of flow of the fluid in the tube is v1 the speed of ejection of the liquid through the holes is

Solution
According to equation of continuity, volume of the fluid flowing in the tube must be equal to the volume of the fluid flowing out through the n holes.
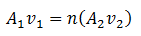
Now the cross-sectional area of the tube of the pump is = πR2
Cross-sectional area of the each of the n holes is = πr2
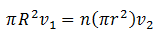
Simplify for v2
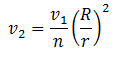
6. In a test experiment on a model aero plane in a wind tunnel, the flow speeds on the lower and upper surfaces of the wings are v and √ 2v respectively. If the density of air is ρ and the surface area of the wing is given by A, then the downward force on the wing is

Solution
Let P1 and P2 are pressures below and above the wing. Apply Bernoulli’s Principle in both cases and subtract.
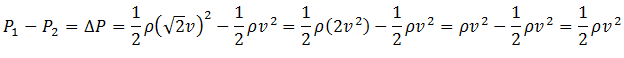
Since force is pressure per unit area, therefore,

7. A rectangular tank is filled completely with water. When a hole at its bottom is unplugged, the tank is emptied in time T. If the tank is half filled with water, it will be emptied in time,

Solution
By Torricelli’s Theorem, if the height of the tank is ‘h’, then the velocity of efflux when the hole at the bottom is unplugged, is given by
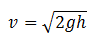
So if T is the time to empty the whole tank of height h, then
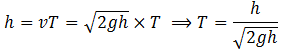
Now if the tank is half-filled, the height h’ is h/2. Apply Torricelli’s theorem in this case, the velocity will be
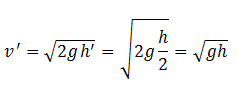
The time required to empty the tank is
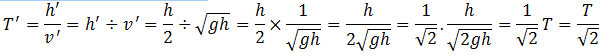
8. Two capillary tubes A and B of equal radius ra = rb = r and equal length la = lb = l are held horizontally. When the same pressure difference P is maintained across such tube, the rate of flow of water in each is Q. If the tubes are connected in series and the same pressure difference P is maintained across the combination, the rate of flow through the combination will be

(A capillary tube is a narrow tube)
Hint: Under the same conditions of pressure and nature of fluid, the same amount of fluid will be flowing through the series combination of the tubes.
9. For spherical objects of uniform density made of the same material but of different radii. Which of the following graphs can best represent the relationship between terminal velocity and radius of the sphere, if each time allowed to fall through same fluid from same height.
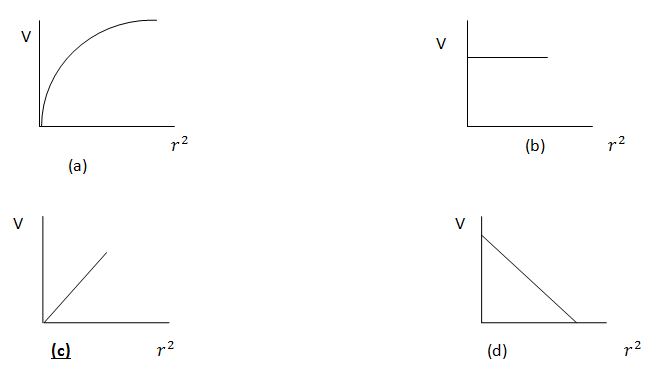
Solution
The relationship between terminal velocity and radius of the sphere is given by
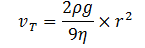
If the fluid is the same, ρ is constant and for same height, g is constant. Therefore, the term 2ρg/η is constant and vT∝ r2. This means, an increase in the radius of the sphere gives a smooth increase in the terminal velocity of the sphere. This assertion is fulfilled only in the option (c).
10. A person standing near the track of a fast moving train has tendency to fall toward it because of
- Vibration due to the motion of the train.
- Gravitational force of attraction the person and the train.
- The high speed of the train.
- Some other effect.
Explanation
11. With the increase of temperature viscosity
| (a) Increases | (b) Decreases | (c) Remains same | (d) Doubles |
Explanation: Viscosity is the property of flowing fluid due to which different layers of the fluid opposes one another motion due to friction. When the temperature of the fluid is increased the speed of the fluid also increases indicating a decrease in the viscosity.
12. According to Stoke law, drag force depends upon
| (a) Initial Velocity | (b) Final Velocity | (c) Instantaneous Velocity | (d) Terminal Velocity |
Explanation: Stoke law is given by
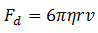
v is the instantaneous velocity.
13. The smooth or steady stream, line flow is known as
| (a) Laminar flow | (b) Turbulent flow | (c) both (a) and (b) | (d) None of the above |
14. Blood has a density
| (a) nearly equal to water | (b) Greater than water | (c) lesser than water | (d) None of the above |
15. The pressure will be low where the speed of the fluid is
| (a) zero | (b) high | (c) low | (d) constant |
Solution
For a horizontal flow of the fluid, Bernoulli’s principle is given by
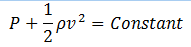
Thus where the pressure is low, the velocity must be high so that the equation has a constant value.
16. Bernoulli’s equation is based upon the law of conservation of
| (a) Mass | (b) Momentum | (c) Energy | (d) None |
Explanation: Bernoulli’s equation is “sum of the pressure, kinetic energy per unit volume and potential energy per unit volume in a steady flow of the ideal fluid is constant at each point along the course of motion.” Thus it is based on the law of conservation of energy.
17. The rain drop falling from the sky reaches the ground with
| (a) Constant terminal velocity | (b) Constant gravitational acceleration | (c) Variable acceleration | (d) Acceleration greater than g |
