Question 1: Show that the motion of mass attached to a spring executes SHM.
ANSWER
Simple Harmonic Motion
The repeated motion of a body about a fixed point is called Simple Harmonic Motion.
Spring mass system and S.H.M
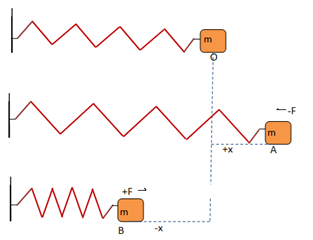
Consider a body of mass ‘m’ attached with a spring at one end and the other end of the spring is fixed to a stable support as shown in the figure. The body is lying on a smooth surface. Suppose the initial position when there is no stress in the spring, is ‘O’. This is called the equilibrium position of the mass. Now let the mass is moved to the right with a force F (= ma) and its new position is ‘A’. This is called the extreme position. The spring will exert a force to restore its position, called restoring force. The restoring force depends upon the nature of the spring, which again depends upon the spring’s constant ‘k’ of the particular spring. (By nature of the spring, we mean the material of which the spring is formed, its geometrical shape, diameter etc.). If ‘x’ is the distance of the body from its mean position, the restoring force of the spring is given by F = -kx and is equal to the force F applied to the mass. Therefore,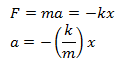
As k and m are both constants, therefore,![]() Now let’s see what this proportionality says.
Now let’s see what this proportionality says.
At the extreme position A, x has maximum value and maximum deceleration.
At point O the displacement x becomes zero and so do the acceleration. However, due to the inertia the mass continuous to move forward and displacement also increases. At the extreme point B the displacement has maximum value and so do the acceleration (negative) and the process is repeated in the same way. Therefore, in case of mass attached to a spring,
- Motion of the body is repeating.
- Acceleration of the body is proportional to its displacement from the mean position.
- Acceleration is always directed toward the mean position.
These are the characteristics of SHM. Therefore, the motion of a mass attached to a spring is Simple Harmonic Motion.

Pingback:projection of a body in circular motion executes SHM … msa – msa
Pingback:index-lq7-p11 – msa
Pingback:Comprehensive Questions, Waves, Physics 11 (new course) … msa – msa