Question 2: Prove that the projection of a body motion in a circle describes SHM.
ANSWER
Projection of circular motion as SHM
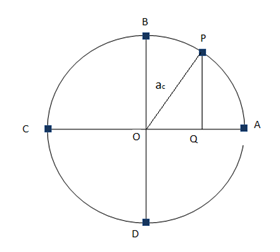
Let an object is moving along a circular path as shown in the figure. Suppose the angular velocity of the body is ω and the radius of the circle in which it moves is ‘r’.
In order to prove that the projection of the object executes simple harmonic motion, we have to show that the motion of the projection of the object obeys the equation of SHM, i-e, ![]() .
.
(Note that if we draw perpendicular from the position of the object at any instant on the diameter of the circle, the point where it meets the diameter is called the projection of the object).
Therefore, if the object is at point ‘A’ on the circle, its projection is also at the point ‘A’. (See the fig). When the object moves along the circle and reaches some point, say ‘P’, its projection is at ‘Q’. When it moves to the point ‘B’ on the circle, its projection is on the center ‘O’ of the circle. At point ‘C’, the projection of the particle is also on ‘C’. At point D, it is again on ‘O’ and when it reaches to point ‘A’ again, the projection is at ‘A’. This means that as the object P moves along the circle, its projection ‘Q’ vibrates along the diameter of the circle executing SHM. This motion has time period as well as frequency.
Now we have to show that the acceleration ax of the projection is directed toward the center and that, a ∝-x, where ‘x’ is the distance from the center along the diameter.
If ![]() is the centripetal acceleration of the object, then its component along the x-axis is accosθ which is in fact the acceleration of the projection of the object. Therefore,
is the centripetal acceleration of the object, then its component along the x-axis is accosθ which is in fact the acceleration of the projection of the object. Therefore,![]()
The direction of this acceleration is toward the mean position, therefore,![]()
Now for the body moving along the circle with constant angular velocity ω, the centripetal acceleration is,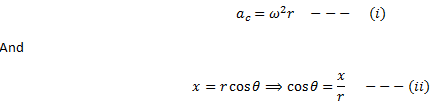
Substituting these values in the equation (A),
So the acceleration of the projection is directly proportional to the displacement and is directed toward the center, therefore, the oscillation is Simple Harmonic Motion.

Pingback:energy-conservation-in-shm – msa
Pingback:motion-of-mass-spring-system – msa
Pingback:Comprehensive Questions, Oscillation, Physics 11 (new course) … msa – msa
Pingback:index-lq7-p11