Question 5: Explain Newton’s formula for the speed of sound.

ANSWER

Newton’s formula for the speed of sound

The distance covered by the sound wave in one second is called the speed of sound.

Sound waves are compressional mechanical waves in nature. So they need a material medium to travel in. Speed of sound waves is, therefore, dependent on the nature of the medium. It is found that;

• Greater the elasticity of the medium, greater is the speed of the sound.
  
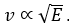
• Lighter (not heavy) the medium (or smaller the density of the medium) faster the sound.
  

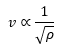
Sound waves consist of alternate compression and rarefaction. In compressional area where the pressure is more, temperature should be high as compared to rarefaction area where the pressure is low.

Newton assumed that the increase in temperature in compression area is promptly neutralized by the decrease in the rarefaction zone and for all practical purposes the temperature of the medium(air) remains constant. This means sound travel through air under isothermal conditions and under such conditions Boyle’s law is applicable.
If the initial pressure is P and ΔP is the small increase in pressure so that the final pressure is P + ΔP. This increment in pressure causes a decrease in the volume, say by ΔV, then the volume changes (decreases) from the initial value V to final value V – ΔV. Boyle’s law states;

 PV = (P + ΔP) (V – ΔV)
               PV = PV – PΔV + VΔP – ΔPΔV
PV – PV = -PΔV + VΔP – ΔPΔV
            0 = -PΔV + VΔP – ΔPΔV

PΔV = VΔP – ΔPΔV

If ΔP is very small, so do ΔV and ΔPΔV is even smaller. So this can be neglected. The above equation becomes;

Calculation based on Newton’s assumption

Using Mercury Barometer, the pressure P can be calculated as

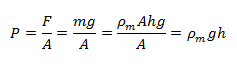
Use this value of P in equation (ii),

However, experimentally proved speed of sound is 332 m/s. Thus the theoretical value (281 m/s) is 16% less than the experimental value (332 m/s). This difference is big enough to be accepted!

Laplace’s Correction

This discrepancy was explained by French scientist Laplace. He argued that the compressions and rarefaction in the longitudinal sound waves cause raise in temperature and cooling effect, respectively.

Sound waves are fast moving waves. On the other hand, air (gases) is a poor conductor of heat. Therefore, during compression air cannot lose heat and cannot gain heat during rarefaction. So the propagation of sound waves through air or gas is an adiabatic one instead of isothermal as Newton assumed. So the changes in air pressure, volume and temperature take place under adiabatic condition. So apply Boyle’s law for adiabatic process,

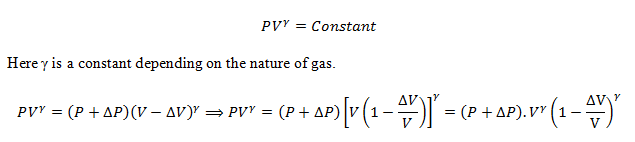
Cancelling P on both sides and re-arranging,

The RHS is Adiabatic Bulk Modulus,E. Therefore,

This value is in agreement with the experimentally calculated value of 332 m/s.