Question 4: What do you mean by stationary waves? Show that as the string vibrates in more and more loops, its frequency increases and wavelength decreases.
ANSWER
Stationary Waves
When two identical waves (and identical waves are those waves having same speeds and amplitudes) travel in opposite directions along the same line, are allowed to superpose with one another, they produce stationary waves.
Explanation
Take a rubber cord (string). Tie fix its one end to a strong support and hold its other end in your hand and move it smoothly up and down with a certain frequency, say f1. Transverse waves are set up along the cord moving away from your hand toward the fixed end. Reaching there, they are reflected with a slightly different shape. When these reflected waves meet the newly generated waves moving away from your hand, they superpose with one another. We note that both the waves are identical (that is the wavelength, speed etc. are same) and moving along the same line (rubber cord) in opposite directions. So they will superpose with one another and will produce a stationary wave in the rubber cord. The whole cord now vibrates in one loop. This waveform doesn’t move in the direction of either wave; produced by the motion of your hand or the one reflected back from the fixed end. Therefore, it is called stationary wave.
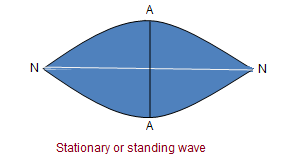
Node
The end points of the stationary wave never vibrate and are called nodes, denoted by ‘N’.
Anti-node
The middle points between two consecutive nodes vibrate with maximum amplitude and are called anti-nodes,denoted by ‘A’.
Wavelength
The distance between two consecutive nodes or anti-nodes is equal to half of the wavelength, denoted by λ/2. So the wavelength in the case of a stationary wave is equal to node to alternate node or the anti-node to alternate anti-node.
(Think about the distance between a node and the next anti-node OR the anti-node and the next node.What is this distance equal to?).
Now gradually increase the frequency of the movement of your hand. It is seen the stationary wave subsides (i-e, falls down or disappears). However, when the frequency of your hand becomes double of the initial frequency, i-e, when the frequency becomes 2f1,the standing wave is seen again; but now with two loops in the rubber cord. This is called second harmonic.
It can be seen that when the frequency is increased to 3f1, 4f1, 5f1… nf1,stationary waves with 3rd, 4th, 5th… nth harmonics are set up and correspondingly, the cord vibrates in 3, 4, 5… n loops.
To show more loops increase frequency and decrease wavelength
Consider a string of length ‘L’. Both its ends are tied fix and the tension in the string is ‘T’. Standing waves can be set up in the string in a number of ways.
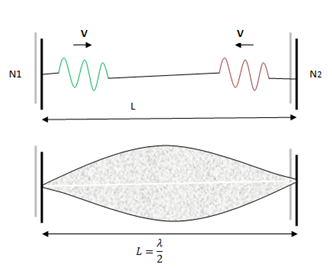
(1)Pull up (pluck) the string in the middle and leave it to vibrate. Two transverse waves are produced in the string; one moves to the right and the other to the left. When they reach the fixed ends, they are reflected back and meet one another at the middle of the string. Here they superpose with one another and a stationary wave is set up in the string. We note,
- The string vibrates in one loop.
- Nodes are at fixed ends.
- One anti-node is at the middle of the string.
- Frequency of the stationary wave is equal to the frequency of the two progressive (or traveling) waves originally produced when the string was plucked. Suppose it is f1.
Now total length of the string is L, which is from N1 to N2. If λ1 is the wavelength of the wave, then,
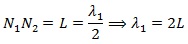
Here λ1 is the length of the wave.
Suppose ‘v’ is the speed of the wave, then we know that, v = fλ
. Apply the above equation to the present situation, v = f1 λ1.
Put the value of λ1 in the above equation,
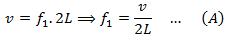
From our previous knowledge, we know that the speed of a transverse wave in a string of mass ‘M’, length ‘L’ and tension ‘T’ is given by,
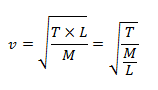
When total mass of the string is divided by the total length of the string, we get mass per unit length of the string. Hence, M/L = m.
Therefore, substituting in equation(A)
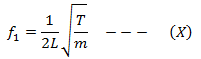
This equation gives the relation of frequency with the length of the string.
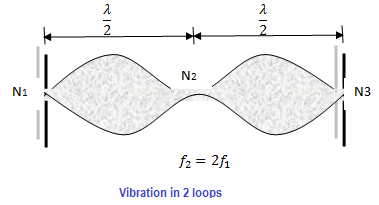
(2) Now suppose the string is plucked at quarter length. This will result the spring vibration in two loops as shown in the figure.
Suppose the vibrating frequency is f2 and the corresponding wavelength of this mode is λ2.Therefore, length of the string is now given by,
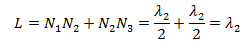
Again from our previous knowledge,
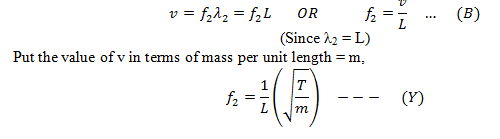
If we compare (X) and (Y), we see in two loops vibration, the frequency is also doubled.
(3) When the string is plucked at one-sixth of its length.
When the string is plucked at one-sixth length, characteristic frequency of oscillation is f3 and the related wavelength is λ3.
In this case, there are three loops in the length ‘L’.
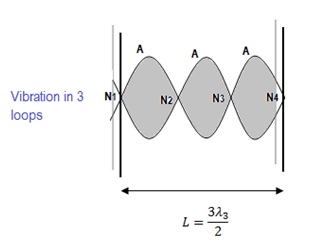
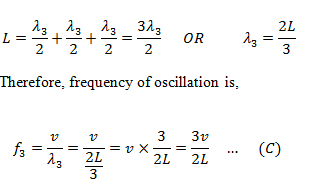
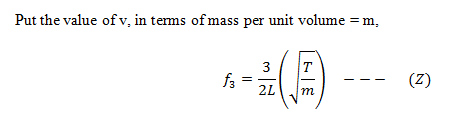
Generalization of frequency relation
Consider the following relations for the frequency of standing wave derived in equations (X), (Y) and (Z).
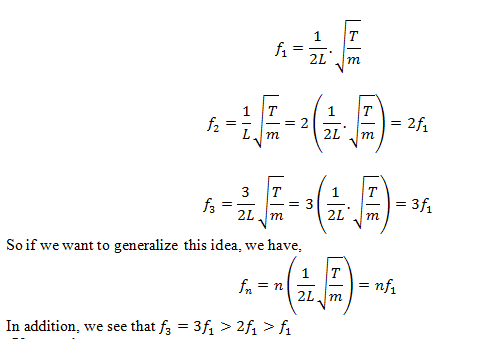
Observations
- For all three calculations made above, length of the string is same, i-e, L.
- For first calculation, there is one loop in the string length L and wave length is λ1.
- For second calculation, 2 loops have been accommodated in the same length ‘L’. This means the wavelength has reduced to half as compared to first calculation.
- For third calculation, 3 loops have been accommodated in string length ‘L’. This means the wavelength has further reduced to one-third of the first calculation (and two-third of the second calculation).
The decrease in wavelength is accompanied by a corresponding increase in frequency. The frequency has increased to f3 = 3f1 = 2f2. So we can conclude from the above observations that when the string vibrates in more and more loops, its frequency increases and wavelength decreases.

Pingback:index-cqs8-p11 – msa
Pingback:Comprehensive Questions on Waves … msa – msa
Pingback:newtons-formula-for-sound – msa
Pingback:crest-trough-node-anti-node-etc – msa