We know that mass of the earth is 6 × 1024 kg.
Newton’s law of universal gravitation is defined as “it is the force (of attraction) every body exerts on every other body which is proportional the product of the masses of the the two bodies and inversely proportional to the square of the distance between them. Since planets have usually huge masses, therefore, normal bodies are always attracted by the planets. Similarly, this force has a separating distance dependence, therefore, for large distances they become negligible and the (small) is said to be out side the gravitational field of the planet.
“the lowest velocity which a body must have in order to escape the gravitational attraction of a particular planet is called escape velocity of that planet.”
Therefore, mass of the moon is,
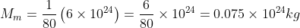
Similarly, radius of the earth = 6.4×106 m.
⇒ Radius of Moon,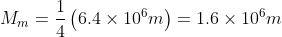
Pingback:Work and Energy, Numerical Problems … msa – msa